| Citation: | Qingyang Zhang, Kaishen Wang, Jingqing Ruan, Yiming Yang, Dengpeng Xing, Bo Xu. Enhancing Multi-agent Coordination via Dual-channel Consensus[J]. Machine Intelligence Research, 2024, 21(2): 349-368. DOI: 10.1007/s11633-023-1464-2 |
Successful coordination in multi-agent systems requires agents to achieve consensus. Previous works propose methods through information sharing, such as explicit information sharing via communication protocols or exchanging information implicitly via behavior prediction. However, these methods may fail in the absence of communication channels or due to biased modeling. In this work, we propose to develop dual-channel consensus (DuCC) via contrastive representation learning for fully cooperative multi-agent systems, which does not need explicit communication and avoids biased modeling. DuCC comprises two types of consensus: temporally extended consensus within each agent (inner-agent consensus) and mutual consensus across agents (inter-agent consensus). To achieve DuCC, we design two objectives to learn representations of slow environmental features for inner-agent consensus and to realize cognitive consistency as inter-agent consensus. Our DuCC is highly general and can be flexibly combined with various MARL algorithms. The extensive experiments on StarCraft multi-agent challenge and Google research football demonstrate that our method efficiently reaches consensus and performs superiorly to state-of-the-art MARL algorithms.
Many real-world multi-agent scenarios can be naturally modeled as partially observable cooperative multi-agent reinforcement learning (MARL)[1] problems. Agents act in a decentralized manner and are endowed with different observations. Uncertainty about the state and action of other agents can hinder coordination, particularly during decentralized sequential execution, leading to catastrophic miscoordination and suboptimal policies.
Successfully achieving coordination in such multi-agent systems often requires agents to achieve consensus[2]. The most common way to accomplish this is through information sharing. By equipping agents with information-sharing skills, many challenges can be alleviated, such as partial observability[3] and non-stationarity[4]. Recent methods either exchange messages explicitly using communication protocols[5–7] or share information implicitly by behavior modeling[8–10] and centralized training[4, 11, 12].
Sharing information explicitly heavily depends on the existence of a communication channel, which may come with limitations such as transmission bandwidth, cost and information delay in real-world scenarios. Implicit sharing needs to either learn a behavior prediction model (behavior modeling) or a centralized learner (centralized training and decentralized execution, CTDE). Behavior modeling enables the environment to appear stationary to an agent, but inaccurate prediction models may lead to significant bias in the agent′s behavior. CTDE enables information to flow in centralized training but lacks mechanisms for information sharing during decentralized execution.
In this work, we propose developing dual-channel consensus (DuCC) to enhance multi-agent coordination. DuCC enables agents to establish a shared understanding of the environmental state by training consensus representations inferred by agents that correlated to the same state to be similar and those of different states to be distinct. This enables agents to overcome the limitations of partial observability and consistently assess the current situation (cognitive consistency), facilitating effective coordination among them. Furthermore, agents independently infer consensus representations during decentralized execution and use them as an additional factor for decision-making. This enables timely information sharing during decentralized execution, without the need for explicit communication. Our method is flexible and can be integrated with various existing MARL algorithms to enhance coordination.
Specifically, we learn consensus representations that reflect DuCC using contrastive representation learning[13]. Contrastive representation learning employs contrastive loss functions to distinguish between similar and dissimilar instances, which is well-suited for establishing common knowledge, as in the case of DuCC. We achieve DuCC through three steps. First, we introduce consensus inference models that map local observations to latent consensus representations, which capture environmental decision-relevant information. Then, we design an inner-agent contrastive representation learning objective to capture slow-changing environmental features and maintain slow information dynamics within each agent over time (inner-agent consensus). We also design an inter-agent contrastive representation learning objective to align inner-agent consensus across multiple agents (inter-agent consensus), thus realizing cognitive consistency[3, 14]. DuCC is considered to be achieved when the learned consensus representations satisfy the two objectives. Finally, we incorporate the consensus representations into MARL algorithms to enhance multi-agent coordination.
We evaluate our method on StarCraft multi-agent challenge[15] and Google research football[16]. The results demonstrate that DuCC significantly improves the performance of various MARL algorithms. In particular, the combination of our method with QMIX, called DuCC-QMIX, outperforms state-of-the-art MARL algorithms. We also design individual consensus metric and group consensus metric to illustrate the efficiency of the two contrastive representation learning objectives in developing DuCC. The visualization of consensus representations shows that our method effectively helps existing MARL algorithms achieve consensus.
Our contribution is three-fold: 1) We propose enhancing multi-agent coordination via dual-channel consensus (DuCC), which includes inner-agent and inter-agent consensus. 2) We design two contrastive representation learning objectives to develop DuCC and propose two metrics to evaluate their effectiveness. 3) We demonstrate our method can be easily integrated with existing MARL algorithms and enhance their performance. Additionally, we provide valuable insights into the effectiveness of our method by visualizing the learned DuCC representations and the DuCC-guided strategies.
In decentralized multi-agent systems, agents often have access to only partial observations of the environment, making it necessary for them to coordinate with other agents to make globally optimal decisions. This coordination can be achieved through explicit or implicit information sharing in MARL[10].
Explicit coordination refers to agents exchanging messages using communication protocols. It can be classified into three types based on how messages are addressed[10]: broadcasting, targeted communication and networked communication. Broadcasting involves sending messages to all agents in the communication channel[4, 17]. For example, an agent′s output can be used as one of the inputs for other agents in the next time step[4], and a multi-agent shared network can broadcast an averaged communication vector between its layers[17]. In targeted communication, agents dynamically determine when[5, 18], what[6, 19], and with whom[7, 20–23] to communicate using attention mechanisms[5, 18], information bottleneck theory[24], or gating mechanisms[25]. Networked communication involves information exchange among agents′ neighbors[21–23]. However, explicit coordination methods heavily rely on a communication channel, which may not always be available or have limitations such as transmission bandwidth, cost and information delay in real-world scenarios.
Implicit coordination refers to agents collecting information from others without communication protocols, such as CTDE and constructing models. CTDE adopts a centralized training process to allow information flow[4, 11, 12, 26–28] across agents. However, during decentralized execution, agents cannot share information due to a lack of information flow mechanisms. Constructing models involves exchanging information through observing teammates′ actions or their effects and predicting the behavior of others by constructing models[8–10, 29]. Although building models of other agents can make the environment appear stationary to an individual agent, the bias of the constructed models may introduce another non-stationarity.
Recently, several methods have been proposed to learn common knowledge[3, 30] to facilitate implicit coordination. These methods can be further classified into two types. The first type relies on prior knowledge for learning or grouping, including MACKRL[14] and NCC-MARL[3]. MACKRL defines common knowledge as subsets of the multi-agent observation space, but this definition is fixed apriori. Additionally, to achieve hierarchical coordination, MACKRL requires learning a hierarchical policy tree that relies on high-level policies to select the group′s joint action, which can negatively impact training efficiency. NCC-MARL proposes neighborhood cognition consistency to develop common knowledge of neighboring agents. However, it does not consider how to partition neighborhoods adaptively and only uses heuristic rules to define neighborhoods. The second type performs end-to-end learning from local observations, including CBMA[30] and COLA[31]. CBMA allows agents to deduce common knowledge from local observations and ensure consistency through a KL-divergence metric. However, CBMA uses variational models based on recurrent neural networks[32] (RNNs) to model the environment and infer common knowledge, which is more difficult to train than our consensus inference models that only require multi-layer perceptrons for implementation. COLA defines common knowledge as discrete one-hot variables with a pre-defined number of classes. Local observations for the same state are grouped into the same common knowledge class. The pre-defined class number restricts the flexibility of common knowledge identification, forcing COLA to rely on RNNs to infer common knowledge precisely from historical episodes. These limitations restrict the applicability of existing algorithms in more general settings. On the contrary, in our method, consensus inference models can be easily implemented using multi-layer perceptrons, and we define consensus representations as continuous variables in a low-dimensional representation space, enabling a more flexible consensus representation identification.
Additionally, none of these methods mentioned above consider learning representations of slow features or capturing slow information dynamics, upon which consensus can be developed. In single-agent reinforcement learning domain, LESSON[33] and HESS[34] utilize triplet loss[35] to learn compressed representations that reflect slow features as subgoals. These subgoals effectively guide exploration in the context of goal-conditioned hierarchical reinforcement learning[36]. Our method considers capturing slow features and maintaining slow information dynamics within each agent over time (inner-agent consensus) and aligning inner-agent consensus across multiple agents (inter-agent consensus) to realize multi-agent coordination. Note that we are the first to consider the slowness feature objective in MARL, based on which we develop DuCC.
There are several works that leverage contrastive representation learning to extract low-dimensional representations from raw inputs in reinforcement learning[37, 38]. Contrastive unsupervised representations for reinforcement learning (CURL)[38] extracts compressed features from pixel inputs using InfoNCE[39] and performs off-policy control on top of the extract features, realizing sample-efficient control in RL. CACL[40] maximizes the mutual information among communicative messages exchanged by different agents within an episode, using supervised contrastive learning[13]. It aligns the message space by pushing messages of the same episode closer together and messages of different episodes further apart. COLA[31] uses self-supervised contrastive representation learning to learn discrete representations of common knowledge. Unlike these methods, our method uses self-supervised contrastive representation learning to learn continuous representations for inner-agent and inter-agent consensus.
The undertakings under consideration are fully cooperative, decentralized partially observable Markov decision processes (Dec-POMDPs)[41]. A Dec-POMDP comprises a tuple G={S,U,P,R,O,Ω,N, γ}. At each time step, each agent i∈I≡{1,⋯,N} is endowed with a local observation oi∈O, which is correlated with a global state s∈S in accordance with the observation function Ωi(s):S→O. We denote o∈O≡ON. The agent then selects an action ui∈U, which in combination with other agents′ actions, forms a joint action u∈U≡UN. The global state is concealed from agents. The joint action u induces an environmental transition as per the transition function P(s′|s,u):S×U×S→[0,1], and results in a global reward R(s,u):S×U→R. The last term γ∈[0,1) is a discount factor. Each agent′s local policy πi(ui|τit) conditions solely on its own action-observation history τit={oi1,ui1,⋯,oit}. Following previous work, we adopt CTDE[4, 11, 12, 26–28] paradigm to enable the learning of decentralized policies in a centralized fashion.
Consensus refers to convergence to a common value[2, 42]. In the domain of multi-agent cooperative control, consensus refers to the convergence of the state variables of individual agents under certain consensus protocols[43, 44]. A consensus protocol is a process of interaction between individuals in a multi-agent system, which describes the information exchange process between each agent and its teammates.
Let xi represent the information of the i-th agent, which needs to be coordinated between agents. A continuous-time consensus protocol can be summarized as
| ˙xi(t)=−∑j∈Ji(t)αij(t)(xi(t)−xj(t)) | (1) |
where Ji(t) represents the set of agents whose information is available to agent i at time t (including agent i itself) and αij denotes a positive time-varying weighting factor. In other words, the information of each agent is driven toward the information of its neighbors at each time. Formula (1) can be written in matrix form as ˙x=−Lx, where L is the graph Laplacian and x=[x1,⋯,xN]T. Correspondingly, a discrete-time consensus protocol can be summarized as
| xit+1=∑j∈Nitβijtxjt | (2) |
where Nit is the set of agents whose information is available to agent i at time t (including agent i itself), βijt>0, and ∑j∈Nitβijt=1. In other words, an agent′s next information is updated as the weighted average of its current information and those of its neighbors. Formula (2) can be written in matrix form as xt+1=Dtxt, where Dt is a stochastic matrix with positive diagonal entries. Consensus is said to be achieved for a team of agents if ‖xit−xjt‖→0 as t→∞,∀i≠j.
In this paper, in addition to developing consensus among multiple agents (inter-agent consensus), we also consider achieving temporal-extended consensus within each agent (inner-agent consensus). This internal consensus refers to the convergence of an agent′s information in immediately adjacent time steps, as represented by ‖xit−xit+δ‖→0 as δ→0,∀i∈I. We will provide a more detailed description of the inner-agent consensus and the inter-agent consensus in Section 4.
We denote the global state as a vector containing L features, i.e., st=[s1t,⋯,sLt], where L∈Z+. According to standard slow feature analysis (SFA)[45, 46], state st can be factored into slow features sslowt and fast features sfastt using a one-step feature change metric Δslt=‖slt−slt+1‖, where l∈[1,L]. Then sslowt are defined as the features with smaller Δslt and vice versa.
Slow features play a vital role in decision-making by capturing decision-relevant information that changes slowly over time[33, 39, 47, 48], such as the relative position between an agent and the goal in a navigation task. On the other hand, fast features, such as the agent′s absolute position, change rapidly but are not essential for decision-making. By focusing on slow features, agents can gain a more meaningful understanding of the system′s decision-relevant dynamics over a longer time scale. This understanding is crucial for identifying causal relationships within the state sequence and making informed decisions with better long-term outcomes.
In POMDPs, each agent only observes oi with a dimension of H∈Z+. Similarly, oit can also be decomposed into slow features oslowt and fast features ofastt using a one-step feature change metric Δoht=‖oht−oht+1‖, where h∈[1,H]. Then oslowt are the features with smaller Δoht and vice versa.
Representation learning[49, 50] refers to the process of learning a parametric mapping from the high-dimensional raw input data (such as image, sound, text, or vector) to a lower-dimensional feature vector (representation). The objective is to capture and extract more useful features that can enhance performance on downstream tasks, effectively acquiring knowledge. There are several core principles for achieving a good representation[49]: distributed abstraction and invariant, etc. Distributed representation implies that representations are expressive and can represent an exponential number of configurations for their size. Abstraction and invariant mean that representations can capture more abstract features that remain unchanged under small changes in input data.
The success of deep learning enables representation learning methods to learn and optimize representations through multiple layers of neural networks. During this process, the model adjusts its network parameters to transform the raw input data into more meaningful and useful representations. These representations store the knowledge that the model gains from the learning process. While distributed representation and abstraction can be partially achieved through deep network architectures, invariant representations are more challenging to achieve. Contrastive learning[51] provides a simple approach to encode these properties within a learned representation[52], and the resulting framework is called contrastive representation learning[53].
Contrastive representation learning has been seen remarkable success in natural language processing[54, 55] and computer vision[56, 57]. It works by contrasting instance similarity among anchor-positive-negative triplets using contrastive loss functions. An anchor denotes a specific data point, often represented as a feature vector or embedding. This anchor is used to establish connections with similar instances (positive instances) and differentiate from dissimilar instances (negative instances). Specifically, each instance (or anchor) is paired with corresponding positive and negative instances in order to learn low-dimensional representations, where anchor-positive pairs are placed closer together, while anchor-negative pairs are separated further apart.
Contrastive representation learning is a more flexible self-supervised learning algorithm compared to others, such as autoencoders[58] or generative models[59]. It has the ability to flexibly extract the required features, such as slow features, by designing positive and negative instances. Furthermore, representation alignment among multiple agents can also be achieved through the design of positive and negative instances, leading to improved consensus development.
In this section, we provide a formal definition of DuCC and describe how to develop and use DuCC to enhance multi-agent coordination within the context of MARL. An overview of our method is presented in Fig. 1. We start by defining two types of consensus, the temporally extended consensus within each agent (inner-agent consensus) and mutual consensus across agents (inter-agent consensus), which together form DuCC. Next, we develop consensus inference models that map local observations to latent consensus representations, capturing environmental decision-relevant information. We then introduce an inner-agent contrastive representation learning objective to develop an inner-agent consensus that captures slow features and maintains slow information dynamics within each agent over time. We also design an inter-agent contrastive representation learning objective to align inner-agent consensus across agents, forming inter-agent consensus. Finally, we discuss how to leverage DuCC to enhance multi-agent coordination.
DuCC consists of two types of consensus: inner-agent consensus and inter-agent consensus. The inner-agent consensus relates to the individual understanding of the slow-changing environmental features at a temporal scale:
Definition 1. Inner-agent consensus refers to the convergence of an agent′s representations z towards reflecting the information of slow features oslow from its local observations. These representations lie in a representation space Z∈Rd:z=χ(oslow,ofast), where d≤H, H is the dimension of local observations, and χ is a representation function.
The inner-agent consensus allows agents to concentrate on slow features, which in turn enables them to develop a more meaningful understanding of the system′s decision-relevant dynamics over a longer time scale. This understanding is critical for identifying causal relationships within the observation sequence and making informed decisions that lead to better long-term outcomes.
In the extreme case where we set the threshold of one-step feature change metric Δoht to zero, the features that remain fixed at different time steps will be identified as slow features. However, they may not provide informative insights for decision-making tasks. Therefore, for inner-agent consensus, we relax the conditions for consensus by allowing some degree of variation in slow features, such that agents can make decisions based on the consensus representations of these decision-relevant informative slow features.
We assume that each team member develops an inner-agent consensus in the consensus representation space Z. Since all agents are related to the same underlying state s and share the same reward function, which significantly influences their decision-making, it is expected that the consensus representations zi∈Z for all i∈I share similarities. As a result, the consensus representations of multiple agents correlated with the same state are clustered in Z, while those of different states are separated.
Definition 2. Inter-agent consensus refers to the convergence of N agents′ consensus representations z= {z1,⋯,zN} towards a common representation z∗ in the consensus representation space Z for state s. This convergence is characterized by zit→z∗t for all i∈I, where z∗t reflects the common information inferred by agents from local observations correlated with st in Z.
Inter-agent consensus reflects the cognitive consistency established among agents. Since both inner-agent consensus and inter-agent consensus are derived from local observations, agents can independently infer consensus representations from their own local observations during decentralized execution, without the need for explicit information exchange. In other words, by striving to reach DuCC, agents can implicitly and timely share information during decentralized execution without requiring explicit communication protocols such as communication channels. This enables agents to coordinate their actions and effectively accomplish shared tasks.
Finally, we arrive at the definition of dual-channel consensus (DuCC) as the convergence of consensus representations towards satisfying both Definitions 1 and 2 in the consensus representation space Z. In the following sections, we will use the term consensus representation to denote the representation z∈Z and consensus space to denote the consensus representation space Z.
We define a consensus inference model ϕi:O→Z for each agent, where Z is the consensus space. We denote the set of all consensus inference models as ϕ={ϕ1,⋯,ϕN}. Each ϕi can be implemented using a multi-layer perceptron. We use contrastive representation learning as the consensus protocol and design two contrastive representation learning objectives JIϕ and JGϕ for training ϕ. We maintain a replay buffer[60] denoted as Bp that stores historical anchor-positive-negative triplets for training ϕ.
Let T denote the maximum episodic length and c∈[1,T] denote a hyperparameter representing the length of a time slice. The value of c should be chosen to positively correlate with T. For instance, if the maximum episodic length T is 100, a suitable range for c might be between 5 and 50. Due to the constraint of Δoht, the slow features corresponding to time intervals less than c change slightly, such as oslowt and oslowt+m, where m≤c, while those corresponding to time intervals greater than or equal to c change obviously, such as oslowt and oslowt+n, where n≥c. We design an inner-agent contrastive representation learning objective JIϕ to train ϕ to capture slow features and ensure that the above relationships are maintained when mapped to the consensus space Z:
| JIϕ(z)=Ezit−Bp,i∈I,t∈[1,T−n]×[−logexp(zit×zit+mβ1)exp(zit×zit+mβ1)+exp(zit×zit+nβ1)] | (3) |
where zit=ϕi(oit), zit+m=ϕi(oit+m), and zit+n=ϕi(oit+n) form an anchor-positive-negative triplet for contrastive representation learning and β1∈R+ is a scalar temperature parameter. We set β1 to 0.1 following [57]. Objective JIϕ abstracts the observation space to a latent consensus space with slow dynamics. JIϕ is minimized during training.
At time step t, we denote zt={z1t,⋯,zNt} as the consensus representations of all agents and z−it as the consensus representations of all agents except the one of the i-th agent. We design an inter-agent learning objective JGϕ to align zt. To achieve this, for each agent i, the consensus representation zit inferred from its local observation oit is treated as an anchor, and the consensus representation z−it inferred from teammates is expected to align with zit, thus forming positive instances. Note that we constitute negative instances for JGϕ using the concept of inner-agent consensus. The intuition behind this is that zjt+n is pushed away from zjt for all j∈I, and zit and zjt are clustered for all i,j∈I. As a result, zjt+n is also pushed away from zit for all j∈I and j≠i. Therefore, z−it+n works as the negative instances. Then JGϕ is defined as follows:
| JGϕ(z)=Ezit−Bp,i∈I,t∈[1,T−n]×[−log1|Pg(zit)|∑zp∈Pg(zit)exp(zit×zpβ2)∑za∈Ag(zit)exp(zit×zaβ2)] | (4) |
where zit is an anchor, Pg(zit)=z−it are the positive instances, Ag(zit)=Pg(zit)∪z−it+n is the set containing both the positive instances Pg(zit) and the negative instances z−it+n, and β2∈R+ is a scalar temperature parameter. We set β2 to 0.1 following [57]. We minimize JGϕ to capture common knowledge among agents′ inner-agent consensus and, therefore, ensure their cognitive consistency.
To accelerate the training procedure, we implement Bp as a prioritized replay buffer[60]. The anchor-positive-negative triplets that poorly fit JIϕ and JGϕ are the most valuable samples, and thus, they should have higher sampling priority. Bp stores the contrastive losses λϕ(z)=JIϕ(z) + JGϕ(z) of the historical anchor-positive-negative triplets from the last round of training as their priority, which are initially set to positive infinity. During centralized training, we sort the triplets in Bp according to their priority and sample the top 30% triplets with higher priority to train ϕ. Then, we update the priority of the sampled triplets to their latest contrastive losses.
Prioritized sampling a batch of anchor-positive-negative triplets from Bp, we simultaneously optimize JIϕ and JGϕ to train ϕ, which allows us to optimize for slow feature capturing and consensus representation alignment jointly. The consensus developed through this approach is referred to as dual-channel consensus (DuCC), which satisfies the definition of DuCC in Section 4.1. Furthermore, the acquired representations implicitly store DuCC knowledge.
Our method can be easily integrated with existing MARL algorithms and enhance their performance. We denote the trainable parameters of a MARL algorithm as ψ and its replay buffer as Bl. We further augment the input of its policy and value functions with consensus representations z outputted by ϕ. The training objective for the DuCC-augmented MARL algorithm is formulated as JMARLψ,ϕ.
The consensus representation augmented policy πiaug is formulated as
| uit=πiaug(τit,zit). | (5) |
During decentralized execution, agents independently infer the consistent consensus representations in real time. Incorporating these inferred representations as an additional factor for decision-making enables agents to achieve implicit coordination without the need for explicit communication.
Denote τs={s1,⋯,sT} as the global state episode. For value-based algorithms, we augment the inputs of the joint action-value function Qtot and the target network ˆQtot using the inferred consensus representations. Then JMARLψ,ϕ takes the following form:
| JMARLψ,ϕ=Eττt,τs−Bl(ytot−Qtot(ττt,ut,zt))2 | (6) |
where ytot=R(st,ut)+γmaxut+1ˆQtot(ττt+1,ut+1,zt+1), zt={z1t,⋯,zNt} is the consensus representations of all agents at t, and ττt={τ1t,⋯,τNt} is the joint action-observation histories of all agents corresponding to an episode at t. For actor-critic algorithms such as MAPPO, we omit the subscript t for simplicity and define the consensus representation-augmented state value function as Vaug(s,z), then JMARLψ,ϕ consists of two parts, including one for the actor:
| Jactor=Eτi,τs−Bl,i∈I[min(δiAi,clip(δi,1−ϵ,1+ϵ)Ai)+S(πiaug(oi,zi))] | (7) |
where δi=πiaug(ui|τi,zi)πiold(ui|τi,zi), πold refers to the older policy, Ai is the advantage function of agent i using generalized advantage estimation (GAE)[61], S is the policy entropy, σ is the entropy coefficient, and ϵ is a constant. The other part of JMARLψ,ϕ is for the critic:
| Jcritic=Eττ,τs∼Blmax[(Vaug(s,z)−ˆR(s,u))2,(clip(Vaug(s,z),Vold(s,z)−ε,Vold(s,z)+ε)−ˆR(s,u))2] | (8) |
where ε is a constant, ˆR(⋅) is the discounted reward-to-go, and Vold refers to the older value function.
The overall training objective is the combination of JIϕ, JGϕ and JMARLψ,ϕ:
| Jtotal=JIϕ+JGϕ+JMARLψ,ϕ. | (9) |
JIϕ, JGϕ and JMARLψ,ϕ are jointly optimized. We minimize Jtotal during training. The overall procedure of our method is summarized in Algorithm 1.
Algorithm 1. Enhance multi-agent coordination via DuCC
Initialize: Policies {πiaug}, i∈I, models ϕ, parameters ψ, buffer Bl and Bp, length c of the time slice, episode interval M.
Output: ψ, ϕ.
1) for episode e=1 to E do
2) Initialize the environment o1←Env.
3) for environments step t=1 to T do
4) Each agent infers zit=ϕi(oit) and selects an action uit=πiaug(τit,zit).
5) Execute the joint action ut and get ot+1, R(st,ut).
6) end for
7) Insert ττ={τ1,⋯,τN} and global state episode τs into Bl.
8) Construct anchor-positive-negative triplets from ττ and add them to Bp.
9) Sample mini-batch from Bl to train ψ and ϕ using JMARLψ,ϕ.
10) if emodM=0 then
11) Sample mini-batch from Bp to train ϕ using JIϕ in (3) and JGϕ in (4).
12) end if
13) Update the priorities of samples in Bp.
14) end for
We conduct experiments on two challenging environments, StarCraft multi-agent challenges (SMAC)[15] and Google research football (GRF)[16], to answer the following questions: 1) Can our method improve performance by enhancing multi-agent coordination? 2) How does our method compare to various implicit and explicit coordination methods? 3) Do the two contrastive representation learning objectives effectively develop consensus? 4) How can our method be integrated with various MARL algorithms? 5) What is the role of each contrastive representation learning objective?
We combine our method with various MARL algorithms, including:
1) Value-based MARL algorithms, including VDN[26], QMIX[11] and QTRAN[62], which operate within the CTDE paradigm and belong to implicit coordination.
2) Actor-critic MARL algorithms, including COMA[63] and MAPPO[64], which operate within the CTDE paradigm and belong to implicit coordination.
3) Explicit coordination MARL algorithms that rely on exchanging messages using communication protocols: CommNet[17], G2ANet[7], NDQ[65] and MAIC[66], which are the state-of-the-art.
4) Implicit coordination MARL algorithms that rely on developing common knowledge: MACKRL[14] and COLA[31], which are the state-of-the-art.
Note that we use the implementations of VDN, QMIX, QTRAN and COMA in Pymarl
The hyperparameters we employ across all tasks in our experiments are listed in Table 1. When combining our method with various MARL algorithms, we do not modify the hyperparameter settings of the original algorithms.
| Hyperparameters | Values |
| Consensus representation dimension d | 20 |
| Length c of time slice | 10 |
| Episode interval M | 100 |
| Temperature parameter β1 | 0.1 |
| Temperature parameter β2 | 0.1 |
| Time step m | 1 |
| Time step n | 10 |
| Batch size for training ϕ | 128 |
| Capacity of the replay buffer Bp (in episodes) | 5000 |
Each consensus inferring model is a fully connected neural network with three layers, where the intermediate layers have sizes of 256 and 128. The dimension of its output (i.e., the dimension of the consensus representation vector d) is 20. We employ the ReLU[67] activation function. Moreover, we use the Adam[68] optimizer with an initial learning rate of 0.0001.
We share parameters between each consensus inference model ϕi,i∈I. This greatly improves sample efficiency, similar to the implementation of VDN, QMIX, QTRAN and COMA in Pymarl, where policies are shared.
StarCraft multi-agent challenge (SMAC) comprises micromanagement scenarios where agents manage decentralized units to move and attack enemies. The local observations consist of distance, relative x and y coordinates, health, shield and unit type information for allied and enemy units within sight range in the circular map area. In the scenarios we used, the observation dimension ranges from 30 (3m) to 285 (27m\_vs\_30m). The action space consists of a set of discrete actions: move [direction], attack [enemy_id], stop and noop. We use the default reward setting for a shaped reward signal calculated from the hit-point damage dealt, killing enemy units and winning the battle.
Based on the homogeneity/heterogeneity of team members and the symmetry/asymmetry of team composition between opponents, SMAC scenarios can be classified into four types: homogeneous and symmetric, such as 3 m, heterogeneous and symmetric, such as 1c3s5z, homogeneous and asymmetric, such as 8 m_vs_9 m, and heterogeneous and asymmetric, such as MMM2 and 10z5b_vs_2s3z, where the letters in these scenarios′ names represent different unit types. Additionally, each task is also assigned a difficulty assessment of easy, hard and super hard. Table 2 presents the details of the scenarios we used in our experiments.
| Name | Ally units | Enemy units | Type | Difficulty |
| 3m | 3 Marines | 3 Marines | Homogeneous symmetric | Easy |
| 8m | 8 Marines | 8 Marines | Homogeneous symmetric | Easy |
| 3s5z | 3 Stalkers 5 Zealots | 3 Stalkers 5 Zealots | Heterogeneous symmetric | Easy |
| 1c3s5z | 1 Colossus 3 Stalkers 5 Zealots | 1 Colossus 3 Stalkers 5 Zealots | Heterogeneous symmetric | Easy |
| 5m_vs_6m | 5 Marines | 6 Marines | Homogeneous asymmetric | Hard |
| 8m_vs_9m | 8 Marines | 9 Marines | Homogeneous asymmetric | Hard |
| 3s_vs_3z | 3 Stalkers | 3 Zealots | Homogeneous asymmetric | Hard |
| 3s_vs_5z | 3 Stalkers | 5 Zealots | Homogeneous asymmetric | Hard |
| 27m_vs_30m | 27 Marines | 30 Marines | Homogeneous asymmetric | Super hard |
| MMM2 | 1 Medivac 2 Marauders 7 Marines | 1 Medivac 3 Marauder 8 Marines | Heterogeneous asymmetric | Super hard |
| 10z5b_vs_2s3z | 10 Zealots 5 Banelings | 2 Stalkers 3 Zealots | Heterogeneous asymmetric | ⋆ |
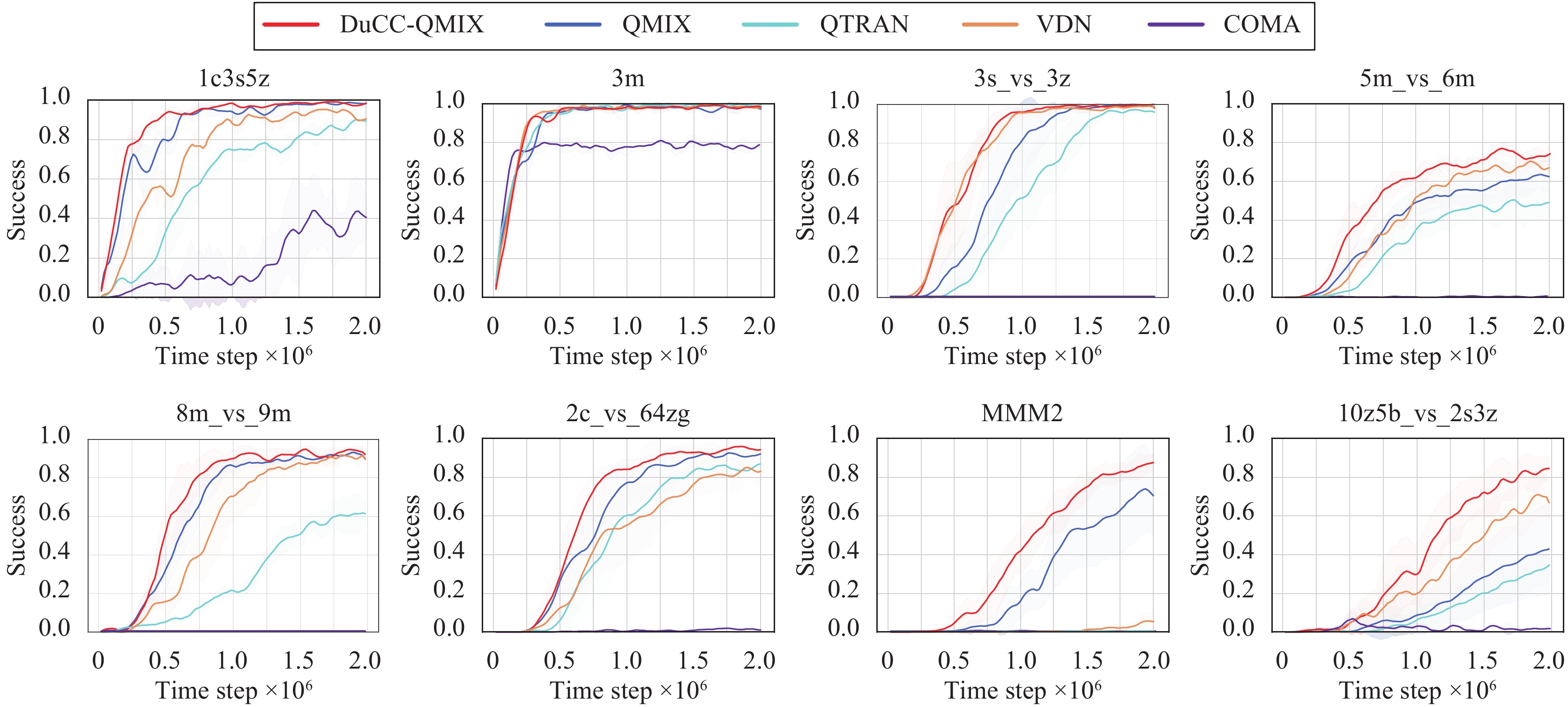
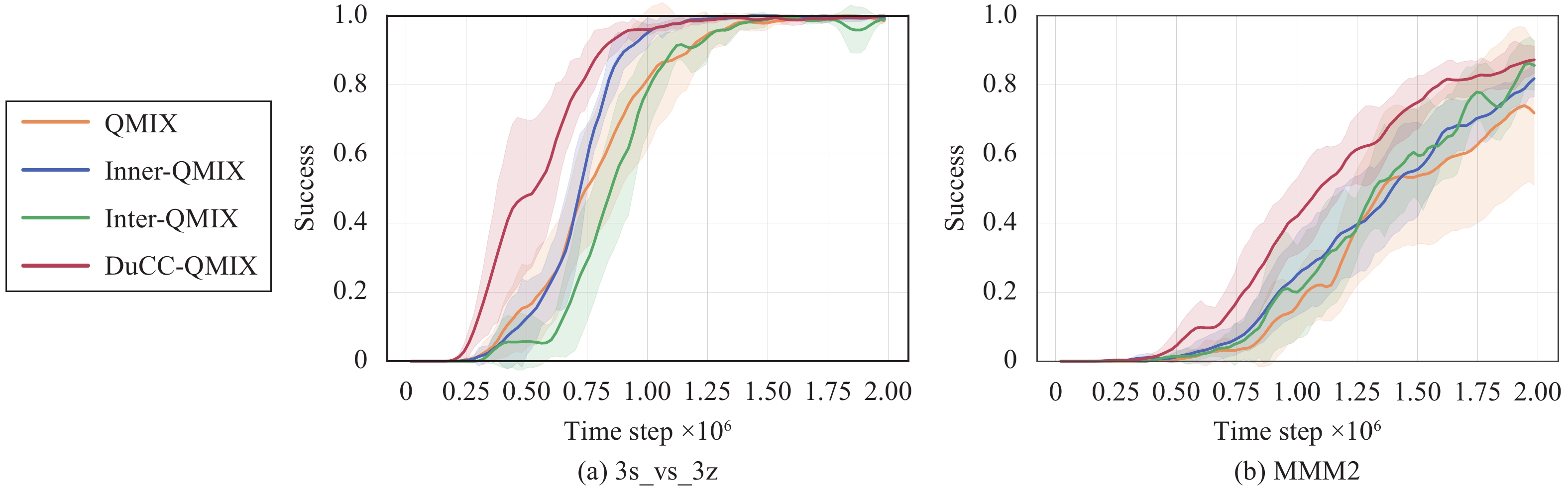
We combine our method with QMIX and test the resulting DuCC-QMIX with value-based MARL algorithms including VDN, QMIX and QTRAN, as well as the actor-critic MARL algorithm COMA, across eight SMAC scenarios. These baselines have demonstrated remarkable performance in SMAC. Fig. 2 shows that DuCC-QMIX significantly improves the performance of QMIX and achieves faster convergence with better asymptotic performance than all the baselines across all eight SMAC scenarios, highlighting the effectiveness of our method in guiding multi-agent coordination. This is because, unlike these CTDE baselines, which can only share information during centralized training, DuCC-QMIX leverages centralized training to develop DuCC and infers consensus representations during decentralized execution to enhance real-time coordination. This ensures timely information sharing during both centralized training and decentralized execution, leading to more efficient coordination among agents.
We further compare DuCC-QMIX with more explicit and implicit coordination algorithms on SMAC. For baselines without open-source code, we mark them with ‡ and report their results from their papers
We first compare DuCC-QMIX with four explicit coordination algorithms: CommNet[17], G2ANet[7], NDQ[65] and MAIC[66]. The experimental results, presented in Table 3, demonstrate that DuCC-QMIX outperforms CommNet, G2ANet, and NDQ in all scenarios, and achieves higher performance than the state-of-the-art MAIC in five scenarios, including both homogeneous and heterogeneous scenarios. These results highlight the superiority of DuCC-QMIX in solving multi-agent coordination problems. Unlike explicit coordination algorithms, which rely on communication protocols, our method is more adaptable and general, as it does not depend on such protocols. This flexibility makes our method suitable for a wide range of tasks without the need for manual tuning or protocol design, leading to stable performance across all scenarios. CommNet broadcasts continuous communication vectors on a common channel. However, to handle a large number of agents, more complex neural models may be required to improve its performance. G2ANet uses a hard-attention mechanism to learn the communication relationship among agents, avoiding the need for broadcasting. However, the complex Bi-LSTM[69] model used to learn the communication weights may contribute to slower convergence. NDQ learns messages that are close to the unit Gaussian distribution, which is a hard constraint that may limit its performance. MAIC learns a targeted teammate model for each agent and constructs a message generator based on these models. However, this dependency relationship may result in unstable performance.
| Scenario | Explicit coordination algorithms (test win rate %) | Implicit coordination algorithms (test win rate %) | |||||
| CommNet | G2ANet | NDQ | MAIC | MACKRL | COLA ‡ | DuCC-QMIX (ours) | |
| 1c3s5z | 24.7 ± 0.2 | 35.4 ± 0.1 | 98.2 ± 0.0 | 99.9 ± 0.0 | 93.7 ± 0.1 | 92.0 | 99.9 ± 0.0 |
| 3m | 49.1 ± 0.4 | 41.9 ± 0.2 | 98.8 ± 0.1 | 99.9 ± 0.0 | 94.1 ± 0.1 | – | 99.9 ± 0.0 |
| 8m | 66.7 ± 0.9 | 49.0 ± 0.5 | 98.1 ± 0.3 | 99.9 ± 0.2 | 93.7 ± 0.4 | – | 99.9 ± 0.2 |
| 3s5z | 1.2 ± 0.1 | 23.4 ± 3.6 | 31.5 ± 3.0 | 95.9 ± 0.6 | 90.4 ± 4.2 | 96.0 | 96.5 ± 0.4 |
| 3s_vs_5z | 3.0 ± 1.0 | 5.3 ± 0.6 | 59.9 ± 7.2 | 71.6 ± 1.5 | 81.5 ± 3.4 | 82.0 | 86.7 ± 1.5 |
| 5m_vs_6m | 2.2 ± 0.4 | 4.2 ± 0.7 | 59.6 ± 6.4 | 64.9 ± 3.2 | 62.0 ± 5.5 | 71.0 | 76.7 ± 2.0 |
| MMM2 | 1.5 ± 0.1 | 1.2 ± 0.1 | 38.5 ± 11.2 | 87.4 ± 3.6 | 59.5 ± 5.0 | 82.0 | 88.9 ± 3.5 |
| 27m_vs_30m | 0.0 ± 0.0 | 0.0 ± 0.0 | 23.6 ± 7.1 | 58.9 ± 5.5 | 39.0 ± 7.0 | 41.0 | 59.4 ± 6.4 |
We then compare DuCC-QMIX with implicit coordination algorithms that develop common knowledge, including MACKRL[14] and COLA[31]. The results are shown in Table 3. DuCC-QMIX achieves the best asymptotic performance in all scenarios. MACKRL learns a hierarchical policy tree that relies on high-level policies to select the group′s joint action, which negatively impacts training efficiency. COLA employs RNNs to infer common knowledge from historical episodes. The RNNs used by COLA result in slower convergence compared to our consensus inference models, which only require multi-layer perceptrons for implementation. Furthermore, COLA defines common knowledge as discrete one-hot variables with a pre-defined number of classes, limiting its flexibility in identifying consensus representations. In contrast, DuCC-QMIX learns continuous consensus representations in a low-dimensional representation space, enabling flexible consensus representation identification. Additionally, none of these implicit coordination methods mentioned above consider learning representations of slow features or capturing slow environmental dynamics, upon which consensus can be developed. In contrast, DuCC-QMIX considers capturing slow features and maintaining slow information dynamics within each agent over time (inner-agent consensus), as well as aligning inner-agent consensus across multiple agents (inter-agent consensus), resulting in superior asymptotic performance across all scenarios.
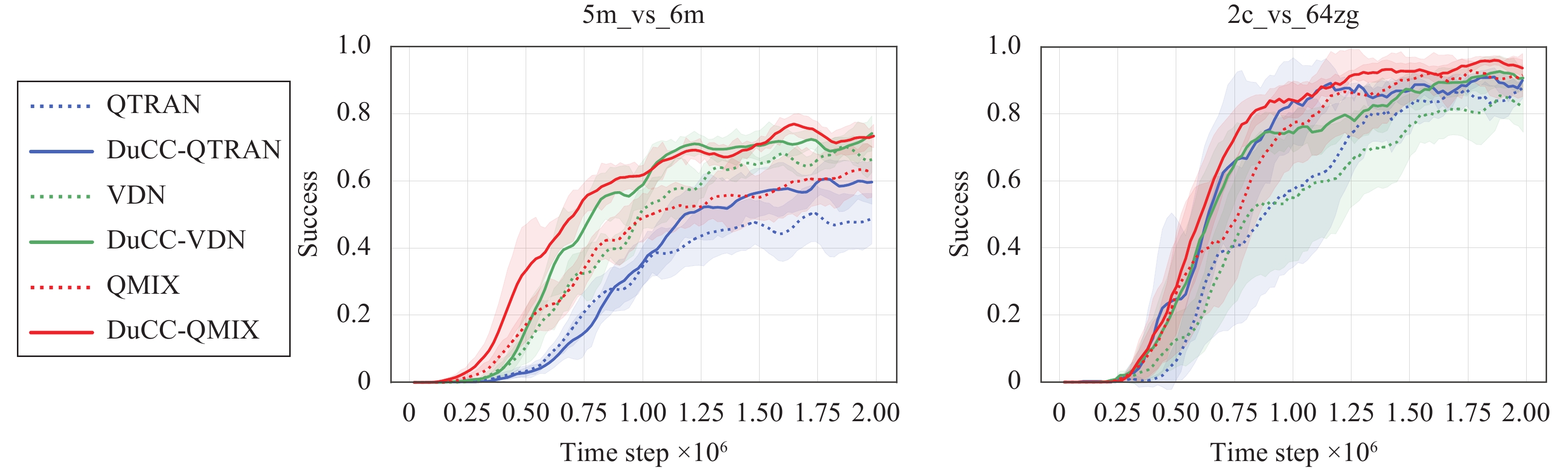
DuCC is algorithm-agnostic in regard to specific MARL algorithms. To evaluate the adaptability of our method, we combine it with VDN and QTRAN and evaluate the resulting DuCC-VDN and DuCC-QTRAN in MMM2 and 2c_vs_64zg of SMAC. As shown in Fig. 3, all the integrated methods outperform the original ones. The faster convergence speed and improved asymptotic performance of DuCC-VDN, DuCC-QTRAN and DuCC-QMIX demonstrate that our method can be flexibly combined with various MARL algorithms to enhance their performance.
Google research football (GRF) provides homogeneous football scenarios that challenge agents to score goals against pre-programmed opponents. Local observations, with a dimension of 115, summarize the coordinates and directions of players and the ball, ball possession, ownership and the current game mode. The action space consists of twenty actions, including idle, move, shoot and pass. Agents receive a reward when they successfully score a goal.
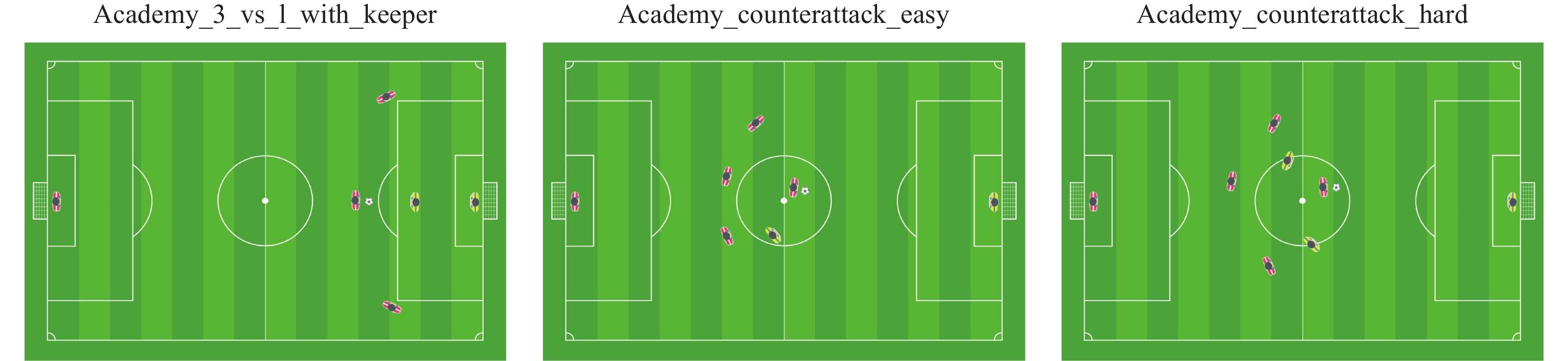
We evaluate our method in three GRF mini-scenarios shown in Fig. 4:
1) Academy_3_vs_1_with_keeper, where players aim to score a goal against an opponent keeper with three offensive players at the edge of the box, with one player on each side and another in the center facing a defender.
2) Academy_counterattack_easy, where players face a 4 versus 1 counter-attack with a keeper while all the remaining players from both teams run back towards the ball.
3) Academy_counterattack_hard, which is similar to the second scenario but is a more challenging 4 versus 2 counter-attack.
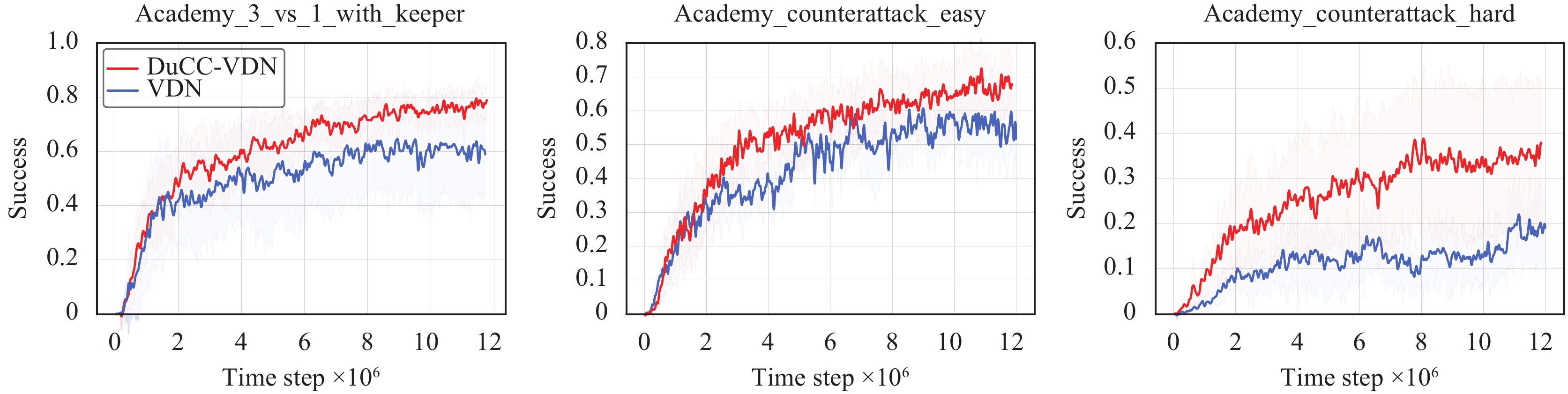
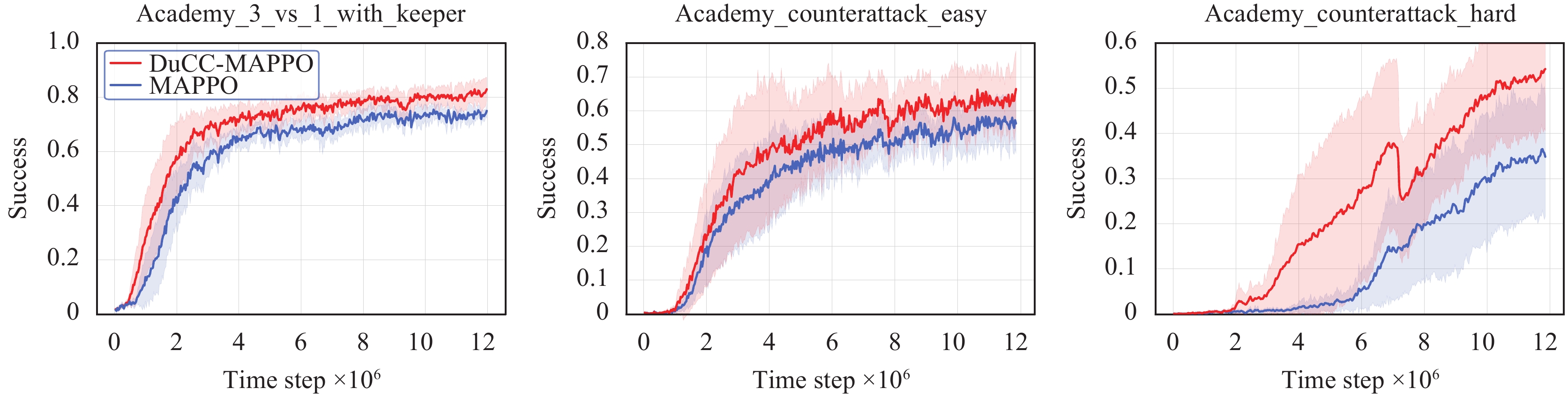
We compare the performance of DuCC-QMIX with value-based MARL algorithms including VDN, QMIX and QTRAN, as well as actor-critic MARL algorithms including COMA and MAPPO across the three GRF scenarios. The results presented in Table 4 demonstrate that DuCC-QMIX significantly improves the performance of QMIX and outperforms all the baseline algorithms across all scenarios. These findings highlight the effectiveness of our method in guiding multi-agent coordination and demonstrate its ability to achieve superior performance in different environments.
| Scenario | MARL algorithms (test win rate %) | |||||
| VDN | QMIX | QTRAN | COMA | MAPPO | DuCC-QMIX (ours) | |
| Academy_3_vs_1_with_keeper | 59.3 ± 4.4 | 62.9 ± 4.2 | 55.6 ± 3.2 | 1.8 ± 0.4 | 74.5 ± 0.5 | 81.4 ± 2.3 |
| Academy_counterattack_easy | 54.4 ± 2.2 | 56.1 ± 1.4 | 52.5 ± 7.2 | 1.7 ± 0.4 | 57.4 ± 1.4 | 72.3 ± 1.5 |
| Academy_counterattack_hard | 20.1 ± 2.2 | 33.2 ± 1.3 | 21.5 ± 6.3 | 0.0 ± 0.0 | 35.8 ± 3.3 | 43.7 ± 1.7 |
We integrate our method with VDN and MAPPO, and evaluate the resulting DuCC-VDN and DuCC-MAPPO in the three GRF scenarios. As shown in Fig. 5, DuCC-VDN achieves an average test win rate improvement of nearly 20% in all scenarios compared to VDN. Similarly, Fig. 6 illustrates that DuCC-MAPPO gained almost 20% in academy_counterattack_hard and 10% in the other scenarios compared to MAPPO. These results indicate that our method can be flexibly integrated with both value-based and actor-critic MARL algorithms to improve their performance.
Our method learns DuCC knowledge through representation learning, which consists of inner-agent consensus knowledge and inter-agent consensus knowledge. DuCC knowledge is implicitly stored in the consensus representations zi=ϕi(oi), for i∈I. By visualizing and analyzing DuCC representations and DuCC-guided strategies, we gain insights into DuCC knowledge, its storage and its utilization.
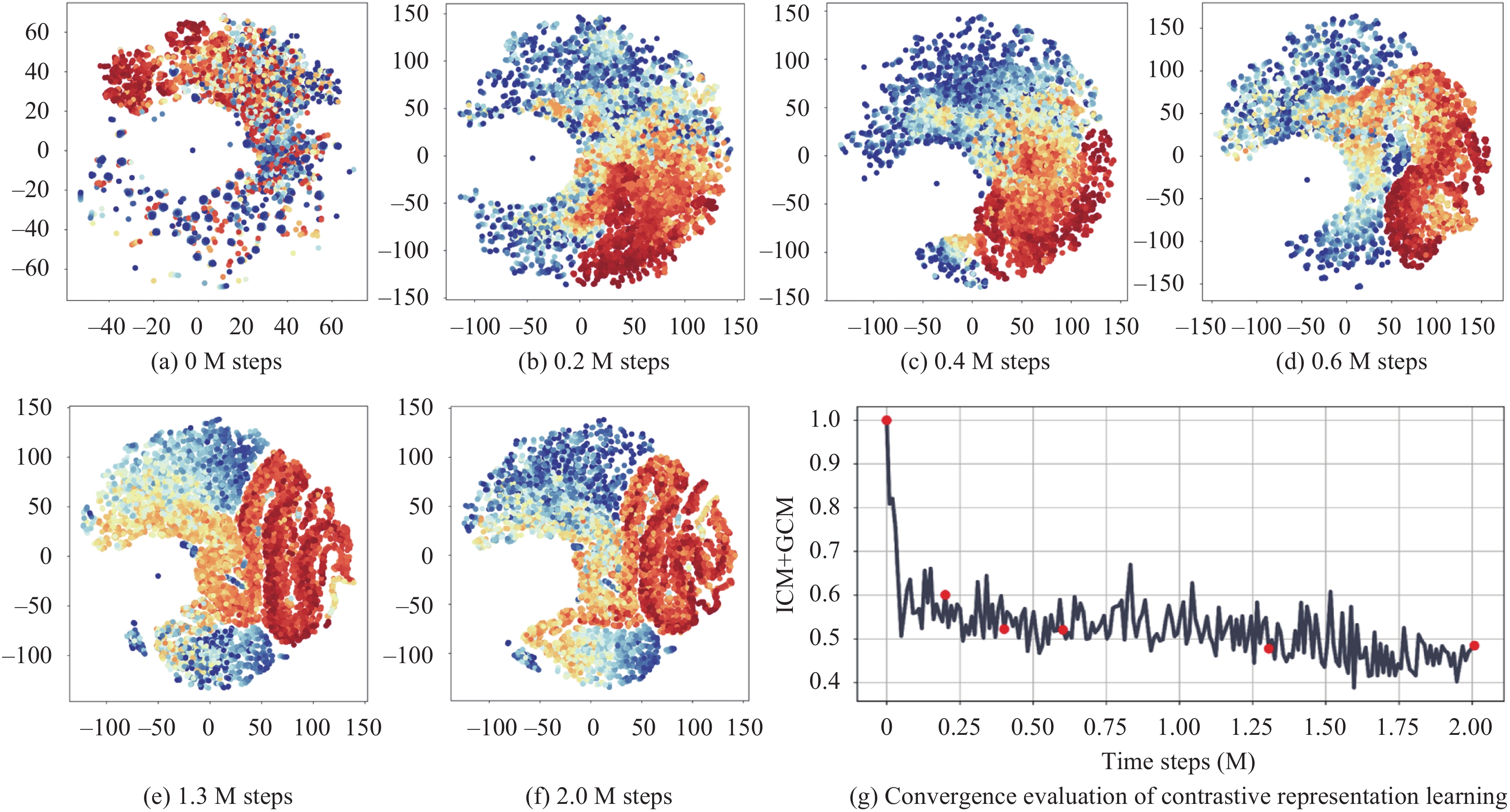
We first visualize DuCC-QMIX′s representation learning process in MMM2, as shown in Fig. 7. We use a gradient of colors from red to blue to represent each agent′s consensus representation episode. At the same time step, the colors for different agents′ representations are the same. Each subfigure presents the results of 50 episodes. We present visualizations of representation distributions for both the early training stages (0 M, 0.2 M, 0.4 M, 0.6 M) and the gradually stabilized representation distributions (1.3 M, 2.0 M) to highlight the formation and the convergence of these distributions, where M represents million. The selection of these specific time steps is based on the normalized convergence evaluation shown in Fig. 7(g), which is calculated using two metrics, individual consensus metric (ICM) and group consensus metric (GCM). Further details regarding this evaluation can be found in Section 5.5.2.
In early stages, our method gradually learns DuCC representations with a regular distribution, which demonstrates the effectiveness of the proposed contrastive representation learning objectives JIϕ and JGϕ in developing DuCC knowledge. As the representation learning progresses, the consensus inference models ϕ continuously update. However, the distribution of representations changes consistently and maintains similarity between neighboring stages. This characteristic of consistent representation distribution allows us to reuse the acquired DuCC knowledge, enabling the agent to make near-optimal decisions and enhancing learning efficiency.
In the mid-to-late training stages, the representation distributions gradually converge. Within an individual representation episode, representations at nearby time steps (indicated by similar colors) have similar values, while at two further time steps (indicated by different colors), the representations keep a distance from each other. These slow dynamics observed in each agent′s consensus representation episode demonstrate that the learned consensus representations successfully contain the inner-agent consensus knowledge. Moreover, within the multi-agent representation episodes, the representations for all agents at the same time step (indicated by the same colors) exhibit a clustering distribution, indicating that the inferred consensus representations of these agents have similar values. This serves as evidence that the learned consensus representations successfully contain the inter-agent consensus knowledge.
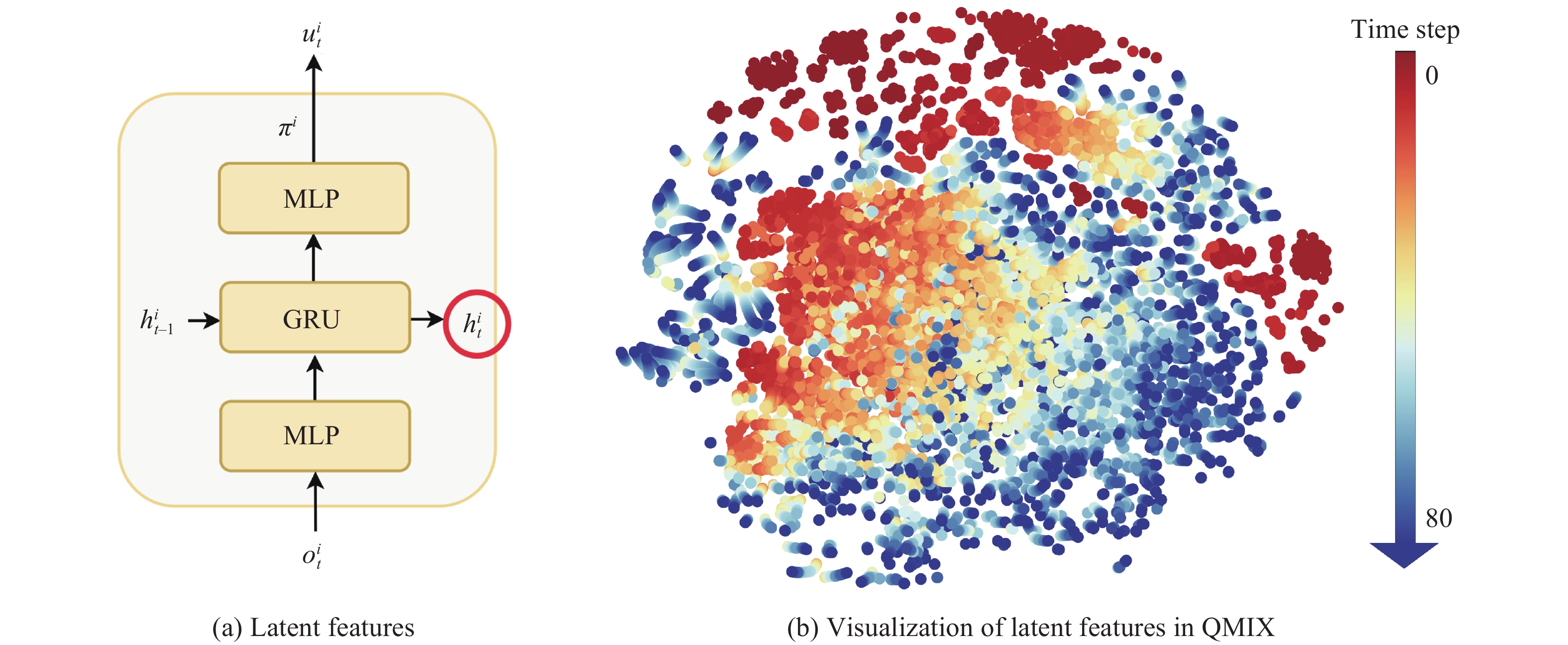
We further compare the DuCC knowledge with the knowledge learned by QMIX. Although QMIX lacks a representation learning module, we can interpret the latent features of agents′ policies as the knowledge it acquires, as shown in Fig. 8(a). The t-SNE results obtained from 50 episodes after training for 2 million steps are presented in Fig. 8(b). We use a gradient of colors from red to blue to represent each agent′s latent feature episode. Compared to the distribution of consensus representations learned by DuCC-QMIX, these features exhibit a disorderly distribution. This once again demonstrates the effectiveness of our method in acquiring DuCC knowledge.
We propose two metrics: individual consensus metric (ICM) and group consensus metric (GCM). ICM measures the quality of the developed inner-agent consensus and takes the following form:
| ICM(ϕ)=Ei∈I,t∈T‖zit−zit+m‖2‖zit−zit+n‖2≥0. | (10) |
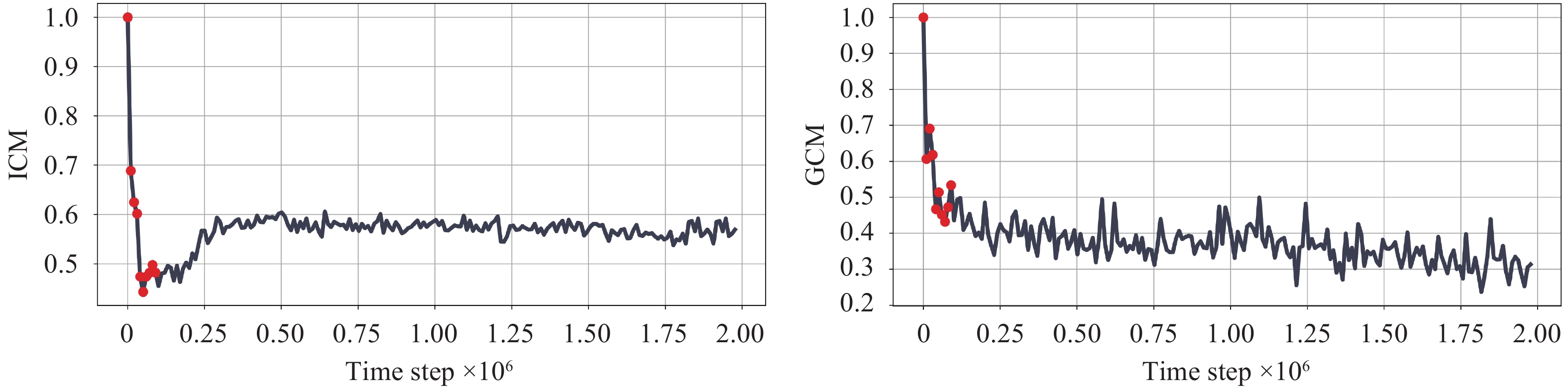
The numerator of ICM is the Euclidean distance between an agent′s consensus representations corresponding to time intervals less than c, while the denominator is the distance between the agent′s consensus representations corresponding to time intervals greater than or equal to c. A small ICM indicates that the agent captures decision-relevant informative slow features from observations and the formation of inner-agent consensus knowledge.
GCM measures the quality of the developed inter-agent consensus. Let ˉzt=Ei∈I(zit) denote the averaged consensus representations of all agents at time step t and ˉz=Ei∈I,t∈T(zit) denote the averaged consensus representations of all agents across the entire episode. Then GCM is defined as
| GCM(ϕ)=Ei∈I,t∈T‖zit−ˉzt‖2‖zit−ˉz‖2≥0. | (11) |
A desirable outcome of JGϕ is for the agents′ consensus representations at each time step t, denoted as zt, to converge, while the consensus representations of all agents at different time steps, i.e., {z1,⋯,zT}, should diverge. Therefore, a smaller GCM is preferred because it indicates the development of inter-agent consensus knowledge and a non-collapsed consensus space. Note that a collapsed consensus space, where all consensus representations cluster in a small region or distribute disorderly will cause GCM to approximate 1.
Fig. 9 shows the normalized evolutions of the ICM and GCM of DuCC-QMIX trained in MMM2. Both metrics show a sharp decline in value during the initial training stages. As training progresses, GCM asymptotically approaches zero. As we loosen the requirements for inner-agent consensus by some variation in slow features to preserve decision-relevant information, ICM converges to a small non-zero value. The rapid convergence of ICM and GCM demonstrates the efficiency of JIϕ in developing inner-agent consensus knowledge and the efficiency of JGϕ in developing inter-agent consensus knowledge.
The utilization of DuCC knowledge occurs in the MARL inference process: At time step t, each agent i∈I uses the consensus inference model ϕi to extract a consensus representation zit=ϕi(oit) from its local observation oit. With the guidance of DuCC knowledge stored in zit, the agent i then selects an action uit=πiaug(τit,zit) using the consensus representation-augmented decentralized policy πiaug.
The update of DuCC knowledge occurs in the MARL training process: The consensus inference models ϕ={ϕ1,⋯,ϕN} are trained through the contrastive representation learning objectives JIϕ and JGϕ, and the DuCC-augmented MARL′s training objective JMARLψ,ϕ. The update of ϕ results in the iteration of DuCC knowledge.
Assuming that an agent extracts a consensus representation zt1=ϕi(ot1) from its local observations ot1 in the inference process. Then, in the training process, zt1 will be used to update ϕ, πaug and Vaug. The agent can then reuse the updated DuCC knowledge to determine the optimal action when encountering the same consensus representation zt1 again. This capability holds whether it is within the same episode or across different episodes, allowing the agent to effectively reuse the learned knowledge.
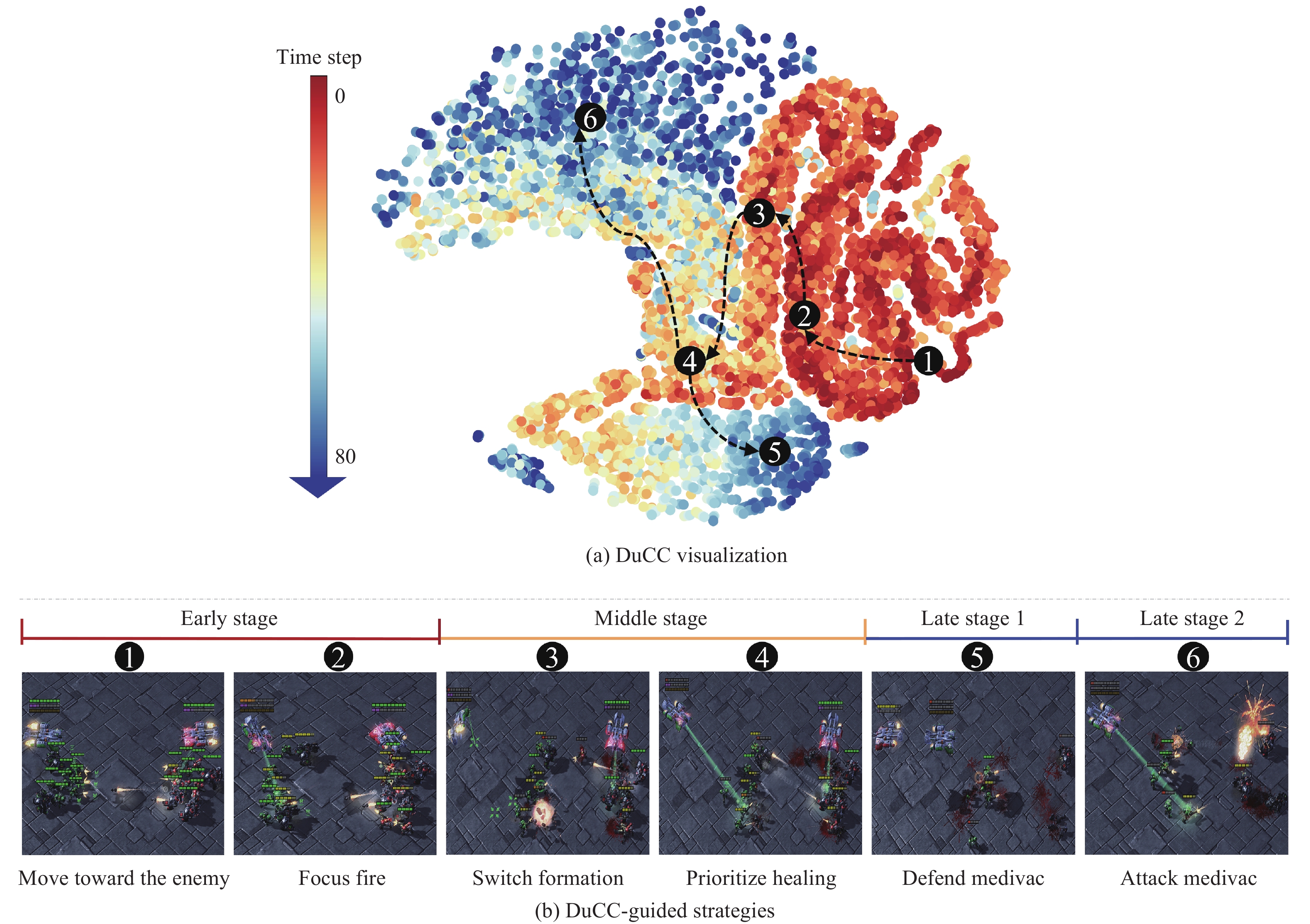
Moreover, due to the neural network′s capacity for generalization, the agent can also make nearly optimal decisions when encountering an unseen consensus representation zt2=ϕi(ot2), as long as zt2 is near zt1 or other previously encountered representations in the consensus space Z. For example, if both zt1 and zt2 are situated in region 2 of Fig. 10(a), then the similar DuCC knowledge embedded in zt1 and zt2 might guide πaug to make similar decisions, such as focus fire, as shown in Fig. 10(b). This generalization ability empowers the agent to efficiently reuse its acquired knowledge to make near-optimal decisions in unexplored states, thereby enhancing learning efficiency and overall performance.
We visualize some DuCC-guided strategies, as shown in Fig. 10(b). During the early stage of the battle, agents move toward the enemy and eliminate enemies one-by-one by focusing fire. As the battle progresses to the middle stage, the team switches the formation, where the wounded agents back off and those with higher health charge ahead. Medivac prioritizes healing the wounded teammates by increasing their health. In the late stage, agents defend or attack the enemy′s medivac based on positions, while continuing to focus fire and prioritize healing. These strategies enable agents to survive longer, maximizing damage to the enemy quickly, indicating the effectiveness of utilizing DuCC knowledge to guide multi-agent coordination. Note that the DuCC representations at the end of the battle are distributed in two locations in the visualization, which is due to the enemy′s medivac adopting two different strategies: remaining active in the enemy camp area or rushing towards our camp area.
Contrastive representation learning objectives. We conduct ablation studies to evaluate the importance of JIϕ and JGϕ in 3s_vs_3z and MMM2. Fig. 11 illustrates that QMIX′s performance is enhanced in both scenarios when using JIϕ alone. This indicates that JIϕ is effective in learning decision-relevant information dynamics. JGϕ improves QMIX′s performance in MMM2 but decreases it in 3s_vs_3z. This is because using JGϕ alone can result in agents having a consistent consensus representation of their local observations (including oslow and ofast). While this does not significantly affect the heterogeneity of agents in a heterogeneous team like MMM2, it may cause homogeneous agents in 3s_vs_3z to converge to similar policies, potentially impacting their performance. Our method simultaneously uses JIϕ and JGϕ to learn slow feature dynamics and align them in the consensus space, achieving the best convergence speed and asymptotic performance in both homogeneous and heterogeneous scenarios. This demonstrates the effectiveness of our method for both types of teams.
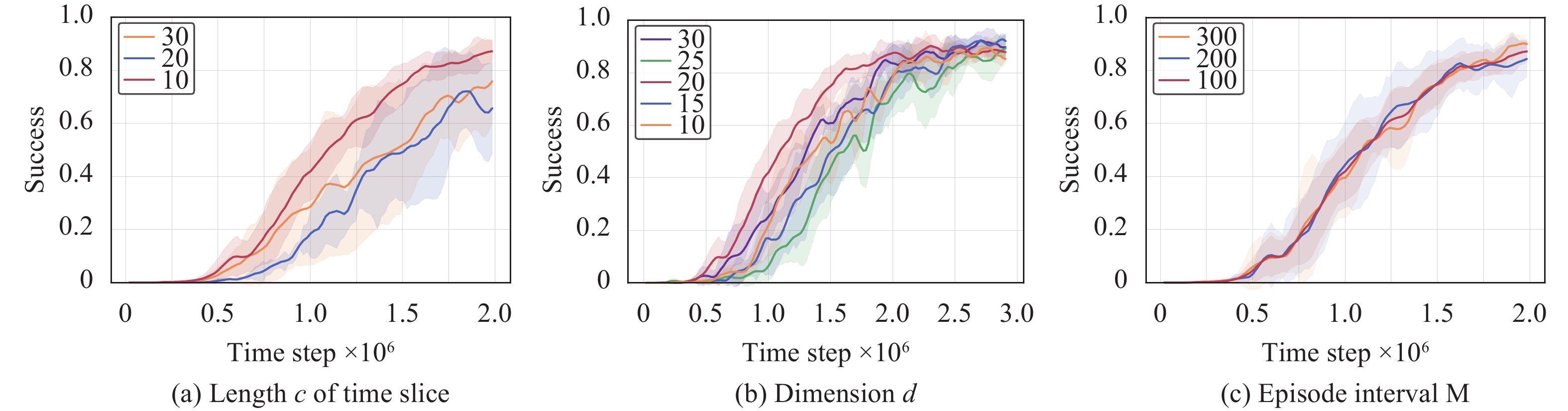
Length c of time slice. c affects the distribution of consensus representations in the consensus space. A divergent distribution of consensus representations enables a more precise consensus representation identification, resulting in more effective decision-making. The results in Fig. 12(a) indicate that DuCC-QMIX performs better when c=10.
Representations dimension d. d determines the degree of information compression, where a smaller value of d leads to greater information loss. The results in Fig. 12(b) indicate that DuCC-QMIX performs better when d=20.
Episode interval M. M affects the stationarity of policy training. A value of M that is too small may lead to frequent updates of consensus representations, and result in unstable policy training. The results in Fig. 12(c) demonstrate the robustness of DuCC-QMIX to various values of M. This robustness can be attributed to the high training efficiency of JIϕ and JGϕ in developing DuCC knowledge.
We first analyze some typical strategies that DuCC-QMIX learns in SMAC in detail as follows:
1) Prioritize attacks on enemies with low health: The agents take enemies down one by one by concentrating attacks on the enemy with the lowest health, as shown in Fig. 13(a). This strategy effectively kills enemies quickly, leading to a swift victory.
2) Formation switching: As charging agents are susceptible to heavy damage from enemy fires, high-health agents adopt a protective formation around low-health teammates. This allows them to shield vulnerable agents from enemy attacks while simultaneously retreating to a safer location. This strategy helps to increase the survival time of the agents while maximizing damage inflicted on the enemies, as depicted in Fig. 13(b).
3) Prioritized healing: The medivac unit has the ability to heal teammates. Fig. 13(c) shows that medivac prioritizes healing teammates who are poor in health or under attack. This strategy helps the marauders and Marines survive longer, thereby maximizing their attacks on enemies.
These strategies demonstrate the effectiveness of DuCC in guiding multi-agent coordination. Note that DuCC-QMIX learns the prioritized attacks on enemies with poor health and formation switching strategies in multiple scenarios, and the prioritized healing strategy in scenarios that include the medivac unit type, such as MMM2. Fig. 13 only illustrates a limited number of scenarios and strategies as examples.
We visualize the strategies learned by QMIX in MMM2 for further comparison. We provide battle replay videos of DuCC-QMIX, named DuCC-QMIX-MMM2, and QMIX, named QMIX-MMM2 in the replay folder in our source code
This paper proposes enhancing multi-agent coordination via dual-channel consensus (DuCC), which comprises temporally extended consensus within each agent (inner-agent consensus) and mutual consensus across agents (inter-agent consensus). We design two contrastive representation learning objectives to simultaneously develop both types of consensus and two metrics to evaluate their efficiency. Extensive experiments on StarCraft multi-agent challenges and Google research football demonstrate that our method outperforms state-of-the-art MARL algorithms and can be flexibly combined with various MARL algorithms to enhance their performance. Finally, we provide visualizations of DuCC and DuCC-guided strategies to facilitate a better understanding of our method.
Bo Xu is an associate editor for Machine Intelligence Research and was not involved in the editorial review, or the decision to publish this article. All authors declare that there are no other competing interests.
This work was supported by the Strategic Priority Research Program of the Chinese Academy of Sciences, China (No. XDA27030300) and the Program for National Nature Science Foundation of China (62073324).
1 https://github.com/oxwhirl/pymarl2 https://github.com/starry-sky6688/MARL-Algorithms
3 We obtain COLA′s results from its paper due to the lack of open-source code, but variance data are unavailable and only percentiles could be estimated.
4 We release our source code at https://github.com/papercode2023/DuCC.
| [1] |
K. Q. Zhang, Z. R. Yang, T. Başar. Multi-agent reinforcement learning: A selective overview of theories and algorithms. Handbook of Reinforcement Learning and Control, K. G. Vamvoudakis, Y. Wan, F. L. Lewis, D. Cansever, Eds., Cham, Germany: Springer, pp. 321–384, 2021. DOI: 10.1007/978-3-030-60990-0_12.
|
| [2] |
W. Ren, R. W. Beard, E. M. Atkins. A survey of consensus problems in multi-agent coordination. In Proceedings of the American Control Conference, Portland, USA, pp. 1859–1864, 2005. DOI: 10.1109/ACC.2005.1470239.
|
| [3] |
H. Y. Mao, W. L. Liu, J. Y. Hao, J. Luo, D. Li, Z. C. Zhang, J. Wang, Z. Xiao. Neighborhood cognition consistent multi-agent reinforcement learning. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, USA, pp. 7219–7226, 2020. DOI: 10.1609/aaai.v34i05.6212.
|
| [4] |
J. N. Foerster, Y. M. Assael, N. de Freitas, S. Whiteson. Learning to communicate with deep multi-agent reinforcement learning. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, pp. 2145–2153, 2016.
|
| [5] |
J. C. Jiang, Z. Q. Lu. Learning attentional communication for multi-agent cooperation. In Proceedings of the 32nd International Conference on Neural Information Processing Systems, Montreal, Canada, pp. 7265–7275, 2018.
|
| [6] |
A. Das, T. Gervet, J. Romoff, D. Batra, D. Parikh, M. Rabbat, J. Pineau. TarMAC: Targeted multi-agent communication. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, USA, pp. 1538–1546, 2019.
|
| [7] |
Y. Liu, W. X. Wang, Y. J. Hu, J. Y. Hao, X. G. Chen, Y. Gao. Multi-agent game abstraction via graph attention neural network. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, USA, pp. 7211–7218, 2020. DOI: 10.1609/aaai.v34i05.6211.
|
| [8] |
A. Rasouli, I. Kotseruba, J. K. Tsotsos. Agreeing to cross: How drivers and pedestrians communicate. In Proceedings of IEEE Intelligent Vehicles Symposium, Los Angeles, USA, pp. 264–269, 2017. DOI: 10.1109/IVS.2017.7995730.
|
| [9] |
Z. Tian, S. H. Zou, I. Davies, T. Warr, L. S. Wu, H. B. Ammar, J. Wang. Learning to communicate implicitly by actions. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, USA, pp. 7261–7268, 2020. DOI: 10.1609/aaai.v34i05.6217.
|
| [10] |
S. Gronauer, K. Diepold. Multi-agent deep reinforcement learning: A survey. Artificial Intelligence Review, vol. 55, no. 2, pp. 895–943, 2022. DOI: 10.1007/s10462-021-09996-w.
|
| [11] |
T. Rashid, M. Samvelyan, C. S. de Witt, G. Farquhar, J. N. Foerster, S. Whiteson. QMIX: Monotonic value function factorisation for deep multi-agent reinforcement learning. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, pp. 4292–4301, 2018.
|
| [12] |
J. H. Wang, Z. Z. Ren, T. Liu, Y. Yu, C. J. Zhang. QPLEX: Duplex dueling multi-agent Q-learning. In Proceedings of the 9th International Conference on Learning Representations, 2021.
|
| [13] |
P. Khosla, P. Teterwak, C. Wang, A. Sarna, Y. L. Tian, P. Isola, A. Maschinot, C. Liu, D. Krishnan. Supervised contrastive learning. In Proceedings of the 34th International Conference on Neural Information Processing Systems, pp. 18661–18673, 2020.
|
| [14] |
C. A. S. de Witt, J. N. Foerster, G. Farquhar, P. H. S. Torr, W. Böehmer, S. Whiteson. Multi-agent common knowledge reinforcement learning. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, Article number 890, 2019.
|
| [15] |
M. Samvelyan, T. Rashid, C. S. de Witt, G. Farquhar, N. Nardelli, T. G. J. Rudner, C. M. Hung, P. H. S. Torr, J. N. Foerster, S. Whiteson. The StarCraft multi-agent challenge. In Proceedings of the 18th International Conference on Autonomous Agents and Multi-Agent Systems, Montreal, Canada, pp. 2186–2188, 2019.
|
| [16] |
K. Kurach, A. Raichuk, P. Stańczyk, M. Zając, O. Bachem, L. Espeholt, C. Riquelme, D. Vincent, M. Michalski, O. Bousquet, S. Gelly. Google research football: A novel reinforcement learning environment. In Proceedings of the 34th AAAI Conference on Artificial Intelligence, New York, USA, pp. 4501–4510, 2020. DOI: 10.1609/aaai.v34i04.5878.
|
| [17] |
S. Sukhbaatar, A. Szlam, R. Fergus. Learning multiagent communication with backpropagation. In Proceedings of the 30th International Conference on Neural Information Processing Systems, Barcelona, Spain, pp. 2252–2260, 2016.
|
| [18] |
A. Singh, T. Jain, S. Sukhbaatar. Learning when to communicate at scale in multi-agent cooperative and competitive tasks. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, USA, 2019.
|
| [19] |
S. Iqbal, F. Sha. Actor-attention-critic for multi-agent reinforcement learning. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, USA, pp. 2961–2970, 2019.
|
| [20] |
Y. Hoshen. VAIN: Attentional multi-agent predictive modeling. In Proceedings of the 31st International Conference on Neural Information Processing Systems, Long Beach, USA, pp. 2698–2708, 2017.
|
| [21] |
K. Q. Zhang, Z. R. Yang, T. Basar. Networked multi-agent reinforcement learning in continuous spaces. In Proceedings of IEEE Conference on Decision and Control, Miami, USA, pp. 2771–2776, 2018. DOI: 10.1109/CDC.2018.8619581.
|
| [22] |
K. Q. Zhang, Z. R. Yang, H. Liu, T. Zhang, T. Basar. Fully decentralized multi-agent reinforcement learning with networked agents. In Proceedings of the 35th International Conference on Machine Learning, Stockholm, Sweden, pp. 5867–5876, 2018.
|
| [23] |
T. S. Chu, S. Chinchali, S. Katti. Multi-agent reinforcement learning for networked system control. In Proceedings of the 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020.
|
| [24] |
R. D. Wang, X. He, R. S. Yu, W. Qiu, B. An, Z. Rabinovich. Learning efficient multi-agent communication: An information bottleneck approach. In Proceedings of the 37th International Conference on Machine Learning, Article number 919, 2020.
|
| [25] |
H. Y. Mao, Z. B. Gong, Z. C. Zhang, Z. Xiao, Y. Ni. Learning multi-agent communication under limited-bandwidth restriction for internet packet routing, [Online], Available: https://arxiv.org/abs/1903.05561, 2019.
|
| [26] |
P. Sunehag, G. Lever, A. Gruslys, W. M. Czarnecki, V. Zambaldi, M. Jaderberg, M. Lanctot, N. Sonnerat, J. Z. Leibo, K. Tuyls, T. Graepel. Value-decomposition networks for cooperative multi-agent learning, [Online], Available: https://arxiv.org/abs/1706.05296, 2017.
|
| [27] |
A. Mahajan, T. Rashid, M. Samvelyan, S. Whiteson. MAVEN: Multi-agent variational exploration. In Proceedings of the 33rd International Conference on Neural Information Processing Systems, Vancouver, Canada, Article number 684, 2019.
|
| [28] |
T. H. Wang, T. Gupta, A. Mahajan, B. Peng, S. Whiteson, C. J. Zhang. RODE: Learning roles to decompose multi-agent tasks. In Proceedings of the 9th International Conference on Learning Representations, 2021.
|
| [29] |
J. Q. Ruan, L. H. Meng, X. T. Xiong, D. P. Xing, B. Xu. Learning multi-agent action coordination via electing first-move agent. In Proceedings of the 32nd International Conference on Automated Planning and Scheduling, Singapore, Singapore, pp. 624–628, 2022. DOI: 10.1609/icaps.v32i1.19850.
|
| [30] |
X. J. Zhang, Y. Liu, H. Y. Mao, C. Yu. Common belief multi-agent reinforcement learning based on variational recurrent models. Neurocomputing, vol. 513, pp. 341–350, 2022. DOI: 10.1016/j.neucom.2022.09.144.
|
| [31] |
Z. W. Xu, B. Zhang, D. P. Li, Z. R. Zhang, G. C. Zhou, H. Chen, G. L. Fan. Consensus learning for cooperative multi-agent reinforcement learning. In Proceedings of the 37th AAAI Conference on Artificial Intelligence, Washington DC, USA, pp. 11726–11734, 2023. DOI: 10.1609/aaai.v37i10.26385.
|
| [32] |
L. R. Medsker, L. C. Jain. Recurrent Neural Networks: Design and Applications, Boca Raton, USA: CRC Press, 1999. DOI: 10.1201/9781003040620.
|
| [33] |
S. Y. Li, L. L. Zheng, J. H. Wang, C. J. Zhang. Learning subgoal representations with slow dynamics. In Proceedings of the 9th International Conference on Learning Representations, 2021.
|
| [34] |
S. Y. Li, J. Zhang, J. H. Wang, Y. Yu, C. J. Zhang. Active hierarchical exploration with stable subgoal representation learning. In Proceedings of the 10th International Conference on Learning Representations, 2022.
|
| [35] |
F. Schroff, D. Kalenichenko, J. Phibin. FaceNet: A unified embedding for face recognition and clustering. In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Boston, USA, pp. 815–823, 2015. DOI: 10.1109/CVPR.2015.7298682.
|
| [36] |
O. Nachum, S. X. Gu, H. Lee, S. Levine. Near-optimal representation learning for hierarchical reinforcement learning. In Proceedings of the 7th International Conference on Learning Representations, New Orleans, USA, 2019.
|
| [37] |
D. Yarats, I. Kostrikov, R. Fergus. Image augmentation is all you need: Regularizing deep reinforcement learning from pixels. In Proceedings of the 9th International Conference on Learning Representations, 2021.
|
| [38] |
M. Laskin, A. Srinivas, P. Abbeel. CURL: Contrastive unsupervised representations for reinforcement learning. In Proceedings of the 37th International Conference on Machine Learning, pp. 5639–5650, 2020.
|
| [39] |
A. van den Oord, Y. Z. Li, O. Vinyals. Representation learning with contrastive predictive coding, [Online], Available: https://arxiv.org/abs/1807.03748, 2018.
|
| [40] |
Y. L. Lo, B. Sengupta. Learning to ground decentralized multi-agent communication with contrastive learning, [Online], Available: https://arxiv.org/abs/2203.03344, 2022.
|
| [41] |
F. A. Oliehoek, M. T. J. Spaan, N. Vlassis. Optimal and approximate Q-value functions for decentralized POMDPs. Journal of Artificial Intelligence Research, vol. 32, pp. 289–353, 2008. DOI: 10.1613/jair.2447.
|
| [42] |
W. Ren, R. W. Beard. Consensus seeking in multiagent systems under dynamically changing interaction topologies. IEEE Transactions on Automatic Control, vol. 50, no. 5, pp. 655–661, 2005. DOI: 10.1109/TAC.2005.846556.
|
| [43] |
L. J. Shan, H. Zhu. Consistency check in modelling multi-agent systems. In Proceedings of the 28th Annual International Computer Software and Applications Conference, Hong Kong, China, pp. 114–119, 2004. DOI: 10.1109/CMPSAC.2004.1342814.
|
| [44] |
J. Y. Yu, L. Wang. Group consensus of multi-agent systems with undirected communication graphs. In Proceedings of the 7th Asian Control Conference, Hong Kong, China, pp. 105–110, 2009.
|
| [45] |
L. Wiskott. Learning invariance manifolds. Neurocomputing, vol. 26-27, pp. 925–932, 1999. DOI: 10.1016/S0925-2312(99)00011-9.
|
| [46] |
L. Wiskott, T. J. Sejnowski. Slow feature analysis: Unsupervised learning of invariances. Neural Computation, vol. 14, no. 4, pp. 715–770, 2002. DOI: 10.1162/089976602317318938.
|
| [47] |
D. Jayaraman, K. Grauman. Slow and steady feature analysis: Higher order temporal coherence in video. In Proceedings of IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, USA, pp. 3852–3861, 2016. DOI: 10.1109/CVPR.2016.418.
|
| [48] |
A. Jansen, M. Plakal, R. Pandya, D. P. W. Ellis, S. Hershey, J. Y. Liu, R. C. Moore, R. A. Saurous. Unsupervised learning of semantic audio representations. In Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing, Calgary, Canada, pp. 126–130, 2018. DOI: 10.1109/ICASSP.2018.8461684.
|
| [49] |
Y. Bengio, A. Courville, P. Vincent. Representation learning: A review and new perspectives. IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 35, no. 8, pp. 1798–1828, 2013. DOI: 10.1109/TPAMI.2013.50.
|
| [50] |
T. Lesort, N. Díaz-Rodríguez, J. F. Goudou, D. Filliat. State representation learning for control: An overview. Neural Networks, vol. 108, pp. 379–392, 2018. DOI: 10.1016/j.neunet.2018.07.006.
|
| [51] |
R. Hadsell, S. Chopra, Y. LeCun. Dimensionality reduction by learning an invariant mapping. In Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, USA, pp. 1735–1742, 2006. DOI: 10.1109/CVPR.2006.100.
|
| [52] |
T. T. Xiao, X. L. Wang, A. A. Efros, T. Darrell. What should not be contrastive in contrastive learning. In Proceedings of the 9th International Conference on Learning Representations, 2021.
|
| [53] |
P. H. Le-Khac, G. Healy, A. F. Smeaton. Contrastive representation learning: A framework and review. IEEE Access, vol. 8, pp. 193907–193934, 2020. DOI: 10.1109/ACCESS.2020.3031549.
|
| [54] |
A. Radford, K. Narasimhan, T. Salimans, I. Sutskever. Improving language understanding by generative pre-training, [Online], Available: https://api.semanticscholar.org/CorpusID:49313245, 2018.
|
| [55] |
J. Devlin, M. W. Chang, K. Lee, K. Toutanova. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, USA, pp. 4171–4186, 2019. DOI: 10.18653/v1/N19-1423.
|
| [56] |
K. M. He, H. Q. Fan, Y. X. Wu, S. N. Xie, R. Girshick. Momentum contrast for unsupervised visual representation learning. In Proceedings of IEEE/CVF Conference on Computer Vision and Pattern Recognition, Seattle, USA, pp. 9729–9738, 2020. DOI: 10.1109/CVPR42600.2020.00975.
|
| [57] |
T. Chen, S. Kornblith, M. Norouzi, G. Hinton. A simple framework for contrastive learning of visual representations. In Proceedings of the 37th International Conference on Machine Learning, Article number 149, 2020.
|
| [58] |
C. Doersch. Tutorial on variational autoencoders, [Online], Available: https://arxiv.org/abs/1606.05908, 2016.
|
| [59] |
D. P. Kingma, D. J. Rezende, S. Mohamed, M. Welling. Semi-supervised learning with deep generative models. In Proceedings of the 27th International Conference on Neural Information Processing Systems, Montreal, Canada, pp. 3581–3589, 2014.
|
| [60] |
T. Schaul, J. Quan, I. Antonoglou, D. Silver. Prioritized experience replay. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2016.
|
| [61] |
J. Schulman, P. Moritz, S. Levine, M. Jordan, P. Abbeel. High-dimensional continuous control using generalized advantage estimation, [Online], Available: https://arxiv.org/abs/1506.02438, 2015.
|
| [62] |
K. Son, D. Kim, W. J. Kang, D. Hostallero, Y. Yi. QTRAN: Learning to factorize with transformation for cooperative multi-agent reinforcement learning. In Proceedings of the 36th International Conference on Machine Learning, Long Beach, USA, pp. 5887–5896, 2019.
|
| [63] |
J. Foerster, G. Farquhar, T. Afouras, N. Nardelli, S. Whiteson. Counterfactual multi-agent policy gradients. In Proceedings of the 32nd AAAI Conference on Artificial Intelligence, New Orleans, USA, pp. 2974–2982, 2018. DOI: 10.1609/aaai.v32i1.11794.
|
| [64] |
C. Yu, A. Velu, E. Vinitsky, J. X. Gao, Y. Wang, A. M. Bayen, Y. Wu. The surprising effectiveness of PPO in cooperative multi-agent games. In Proceedings of the 36th Conference on Neural Information Processing Systems, New Orleans, USA, 2022.
|
| [65] |
T. H. Wang, J. H. Wang, C. Y. Zheng, C. J. Zhang. Learning nearly decomposable value functions via communication minimization. In Proceedings of the 8th International Conference on Learning Representations, Addis Ababa, Ethiopia, 2020.
|
| [66] |
L. Yuan, J. H. Wang, F. X. Zhang, C. H. Wang, Z. Z. Zhang, Y. Yu, C. J. Zhang. Multi-agent incentive communication via decentralized teammate modeling. In Proceedings of the 36th AAAI Conference on Artificial Intelligence, pp. 9466–9474, 2022. DOI: 10.1609/aaai.v36i9.21179.
|
| [67] |
V. Nair, G. E. Hinton. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning, Haifa, Israel, pp. 807–814, 2010.
|
| [68] |
D. P. Kingma, J. Ba. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations, San Diego, USA, 2015.
|
| [69] |
A. Graves, J. Schmidhuber. Framewise phoneme classification with bidirectional LSTM and other neural network architectures. Neural Networks, vol. 18, no. 5–6, pp. 602–610, 2005. DOI: 10.1016/j.neunet.2005.06.042.
|
| [1] | Wen-Jiang Feng, Rong Jiang, Guo-Ling Liu. Distributed Power Control in Cooperative Cognitive Ad hoc Networks[J]. Machine Intelligence Research, 2014, 11(4): 412-417. DOI: 10.1007/s11633-014-0807-4 |
| [2] | Ping-Ping Dai, Cheng-Lin, Liu Fei Liu. Consensus Problem of Heterogeneous Multi-agent Systems with Time Delay under Fixed and Switching Topologies[J]. Machine Intelligence Research, 2014, 11(3): 340-346. DOI: 10.1007/s11633-014-0798-1 |
| [3] | Lin-Lin Ou, Jun-Jie Chen, Dong-Mei Zhang, Wei-Dong Zhang. Distributed H∞ PID Feedback for Improving Consensus Performance of Arbitrary-delayed Multi-agent System[J]. Machine Intelligence Research, 2014, 11(2): 189-196. DOI: 10.1007/s11633-014-0780-y |
| [4] | Ya-Kun Zhu, Xin-Ping Guan, Xiao-Yuan Luo. Finite-time Consensus for Multi-agent Systems via Nonlinear Control Protocols[J]. Machine Intelligence Research, 2013, 10(5): 455-462. DOI: 10.1007/s11633-013-0742-9 |
| [5] | Xiao-Cheng Wang, Xin-Ping Guan, Qiao-Ni Han, Zhi-Xin Liu, Kai Ma. A Stackelberg Game for Spectrum Leasing in Cooperative Cognitive Radio Networks[J]. Machine Intelligence Research, 2013, 10(2): 125-133. DOI: 10.1007/s11633-013-0705-1 |
| [6] | Munam Ali Shah, Sijing Zhang, Carsten Maple. An Analysis on Decentralized Adaptive MAC Protocols for Cognitive Radio Networks[J]. Machine Intelligence Research, 2013, 10(1): 46-52 . DOI: 10.1007/s11633-013-0695-z |
| [7] | Jing Yan, Xin-Ping Guan, Xiao-Yuan Luo, Fu-Xiao Tan. Target Tracking and Obstacle Avoidance for Multi-agent Networks with Input Constraints[J]. Machine Intelligence Research, 2011, 8(1): 46-53. DOI: 10.1007/s11633-010-0553-1 |
| [8] | Jing Yan, Xin-Ping Guan, Fu-Xiao Tan. Target Tracking and Obstacle Avoidance for Multi-agent Systems[J]. Machine Intelligence Research, 2010, 7(4): 550-556. DOI: 10.1007/s11633-010-0539-z |
| [9] | Hai-Tao Zhang, Fang Yu, Wen Li. Step-coordination Algorithm of Traffic Control Based on Multi-agent System[J]. Machine Intelligence Research, 2009, 6(3): 308-313. DOI: 10.1007/s11633-009-0308-z |
| [10] | Hui Yu, Yong-Ji Wang. Stable Flocking Motion of Mobile Agents Following a Leader in Fixed and Switching Networks[J]. Machine Intelligence Research, 2006, 3(1): 8-16. DOI: 10.1007/s11633-006-0008-x |
| Hyperparameters | Values |
| Consensus representation dimension d | 20 |
| Length c of time slice | 10 |
| Episode interval M | 100 |
| Temperature parameter β1 | 0.1 |
| Temperature parameter β2 | 0.1 |
| Time step m | 1 |
| Time step n | 10 |
| Batch size for training ϕ | 128 |
| Capacity of the replay buffer Bp (in episodes) | 5000 |
| Name | Ally units | Enemy units | Type | Difficulty |
| 3m | 3 Marines | 3 Marines | Homogeneous symmetric | Easy |
| 8m | 8 Marines | 8 Marines | Homogeneous symmetric | Easy |
| 3s5z | 3 Stalkers 5 Zealots | 3 Stalkers 5 Zealots | Heterogeneous symmetric | Easy |
| 1c3s5z | 1 Colossus 3 Stalkers 5 Zealots | 1 Colossus 3 Stalkers 5 Zealots | Heterogeneous symmetric | Easy |
| 5m_vs_6m | 5 Marines | 6 Marines | Homogeneous asymmetric | Hard |
| 8m_vs_9m | 8 Marines | 9 Marines | Homogeneous asymmetric | Hard |
| 3s_vs_3z | 3 Stalkers | 3 Zealots | Homogeneous asymmetric | Hard |
| 3s_vs_5z | 3 Stalkers | 5 Zealots | Homogeneous asymmetric | Hard |
| 27m_vs_30m | 27 Marines | 30 Marines | Homogeneous asymmetric | Super hard |
| MMM2 | 1 Medivac 2 Marauders 7 Marines | 1 Medivac 3 Marauder 8 Marines | Heterogeneous asymmetric | Super hard |
| 10z5b_vs_2s3z | 10 Zealots 5 Banelings | 2 Stalkers 3 Zealots | Heterogeneous asymmetric | ⋆ |
| Scenario | Explicit coordination algorithms (test win rate %) | Implicit coordination algorithms (test win rate %) | |||||
| CommNet | G2ANet | NDQ | MAIC | MACKRL | COLA ‡ | DuCC-QMIX (ours) | |
| 1c3s5z | 24.7 ± 0.2 | 35.4 ± 0.1 | 98.2 ± 0.0 | 99.9 ± 0.0 | 93.7 ± 0.1 | 92.0 | 99.9 ± 0.0 |
| 3m | 49.1 ± 0.4 | 41.9 ± 0.2 | 98.8 ± 0.1 | 99.9 ± 0.0 | 94.1 ± 0.1 | – | 99.9 ± 0.0 |
| 8m | 66.7 ± 0.9 | 49.0 ± 0.5 | 98.1 ± 0.3 | 99.9 ± 0.2 | 93.7 ± 0.4 | – | 99.9 ± 0.2 |
| 3s5z | 1.2 ± 0.1 | 23.4 ± 3.6 | 31.5 ± 3.0 | 95.9 ± 0.6 | 90.4 ± 4.2 | 96.0 | 96.5 ± 0.4 |
| 3s_vs_5z | 3.0 ± 1.0 | 5.3 ± 0.6 | 59.9 ± 7.2 | 71.6 ± 1.5 | 81.5 ± 3.4 | 82.0 | 86.7 ± 1.5 |
| 5m_vs_6m | 2.2 ± 0.4 | 4.2 ± 0.7 | 59.6 ± 6.4 | 64.9 ± 3.2 | 62.0 ± 5.5 | 71.0 | 76.7 ± 2.0 |
| MMM2 | 1.5 ± 0.1 | 1.2 ± 0.1 | 38.5 ± 11.2 | 87.4 ± 3.6 | 59.5 ± 5.0 | 82.0 | 88.9 ± 3.5 |
| 27m_vs_30m | 0.0 ± 0.0 | 0.0 ± 0.0 | 23.6 ± 7.1 | 58.9 ± 5.5 | 39.0 ± 7.0 | 41.0 | 59.4 ± 6.4 |
| Scenario | MARL algorithms (test win rate %) | |||||
| VDN | QMIX | QTRAN | COMA | MAPPO | DuCC-QMIX (ours) | |
| Academy_3_vs_1_with_keeper | 59.3 ± 4.4 | 62.9 ± 4.2 | 55.6 ± 3.2 | 1.8 ± 0.4 | 74.5 ± 0.5 | 81.4 ± 2.3 |
| Academy_counterattack_easy | 54.4 ± 2.2 | 56.1 ± 1.4 | 52.5 ± 7.2 | 1.7 ± 0.4 | 57.4 ± 1.4 | 72.3 ± 1.5 |
| Academy_counterattack_hard | 20.1 ± 2.2 | 33.2 ± 1.3 | 21.5 ± 6.3 | 0.0 ± 0.0 | 35.8 ± 3.3 | 43.7 ± 1.7 |