| Citation: | Ying Li, De Xu. Skill Learning for Robotic Insertion Based on One-shot Demonstration and Reinforcement Learning[J]. Machine Intelligence Research, 2021, 18(3): 457-467. DOI: 10.1007/s11633-021-1290-3 |
Recently, precision assembly and manipulation have attracted much attention, and been widely used in micro-electromechanical systems (MEMS) and industrial applications[1-4]. The contact force between components, provided with the force sensor, should be kept within a limited range to guarantee the safety.
Peg in hole assembly is a common assembly task and automatic assembly methods have attracted much attention. Generally, the assembly control methods can be classified into model-based methods and model-free methods. The former have been widely used in assembly tasks. In order to accomplish dual peg in hole assembly, Zhang et al.[5] analyzed the contact states and established the relationship between contact state and contact force. The jamming state was analyzed quantitatively and the corresponding control strategies were developed. In order to assemble three objects together, Liu et al.[6] modelled the contact states between each two components as a probability distribution. The three objects were adjusted simultaneously. Chen et al.[7] developed an error recovery method for wiring harness assembly. The dynamic model of mating connectors on printed circuit board (PCB) is established and the smooth insertion is achieved with moment control. The components in the above methods are rigid. If the components are deformable, the insertion tasks will become more difficult and the contact states will be more complex. Xing et al.[8] presented an efficient assembly method for multiple components connected parallel by spring. An optimization method was developed based on the spring model. Efficiency is an important factor and a passive alignment principle-based method was employed to accomplish assembly tasks with deformable components[9].
However, the above methods are mainly based on mathematical description of contact states which may contain errors. The real contact states are far more complex and the precise model can hardly be obtained. Therefore, model-free precision insertion methods are highly needed.
Recently, reinforcement learning (RL), combined with deep learning, has shown its great potential in the field of artificial intelligence[10] and continuous control has been realized in simulated physics tasks[11]. RL becomes a promising approach for robotic precision assembly[12,13]. Inoue et al.[14] proposed a Q-learning-based method for assembly with robot arm, and long short term memory (LSTM) layers were used to approximate the Q-function. Li et al.[15] presented a robot acquisition method for assembly process. Unlike others, the reward function employed a two-classification support vector machine (SVM) model to determine whether the assembly is successful. However, the actions in the above methods are discrete and continuous actions are more suitable for the assembly process. Fan et al.[16] presented a learning framework for high precision industrial assembly, which combined the supervised learning and deep deterministic policy gradient (DDPG) based RL. Trajectory optimization served as a semi supervisor to provide initial guidance for the actor-critic. In order to improve training efficiency, Vecerik et al.[17] developed a DDPG-based insertion method, which introduced the human demonstrations into the learning process. Guided by the behavior cloning loss, the actor network can imitate the actions from demonstrations. As for deformable objects, Luo et al.[18] proposed a mirror descent guided policy search (MDGPS) method to insert a rigid peg into a deformable hole. Moreover, available priori knowledge can further improve the performance of RL. For example, Thomas et al.[19] developed a computer aided design (CAD) based RL method for robotic assembly. CAD data can be used to guide the RL by a geometric motion plan.
The above RL-based methods can be used in real robotic assembly tasks. However, there are still some problems should to be solved. Firstly, expert demonstrations can improve the training efficiency[17], but it is tedious and not safe to collect much demonstration data on real robotic systems. It is valuable to use as little demonstration data as possible to guide the training process of RL. Secondly, in order to obtain the optimal action policy, abundant exploration is needed. An efficient exploration strategy can accelerate the training process and random exploration in action space is not enough[14]. Therefore, an efficient exploration strategy for robotic assembly is highly needed. Thirdly, the model is usually trained for specific components[19] and should be retrained when meeting new components in real assembly tasks. The adaptability is an important factor and should be improved to meet the requirements of the real assembly tasks. Furthermore, training RL model on real robotic system is time-consuming and low-efficiency. There is a gap between simulation and real robotic systems. In other words, the models trained in simulation environments cannot be directly used on real robotic systems[20]. The training efficiency can be improved if the gap is bridged.
In this paper, a DDPG-based insertion skill learning framework is proposed for robotic assembly. The main contributions of this work are as follows. 1) The final executed action consists of an expert action learned from one demonstration and a refinement action learned from RL, to improve the insertion efficiency. 2) An episode-step based exploration strategy is proposed to explore state space more efficiently, which views the expert action as a benchmark and adjusts the exploration intensity dynamically. 3) A skill saving and selection mechanism is proposed to improve the adaptability of our method. Trained models for several typical components are saved in the skill pool and the most appropriate model will be selected for insertion tasks for a new component. 4) A simulation environment is established with the help of force Jacobian matrix, which avoids tedious training process on real robotic system.
The rest of this paper is organized as follows. Section 2 introduces the system configuration and problem formation. The insertion skill learning framework is detailed in Section 3. Sections 4 and 5 present the simulation and experiment results, respectively. Finally, this paper is concluded in Section 6.
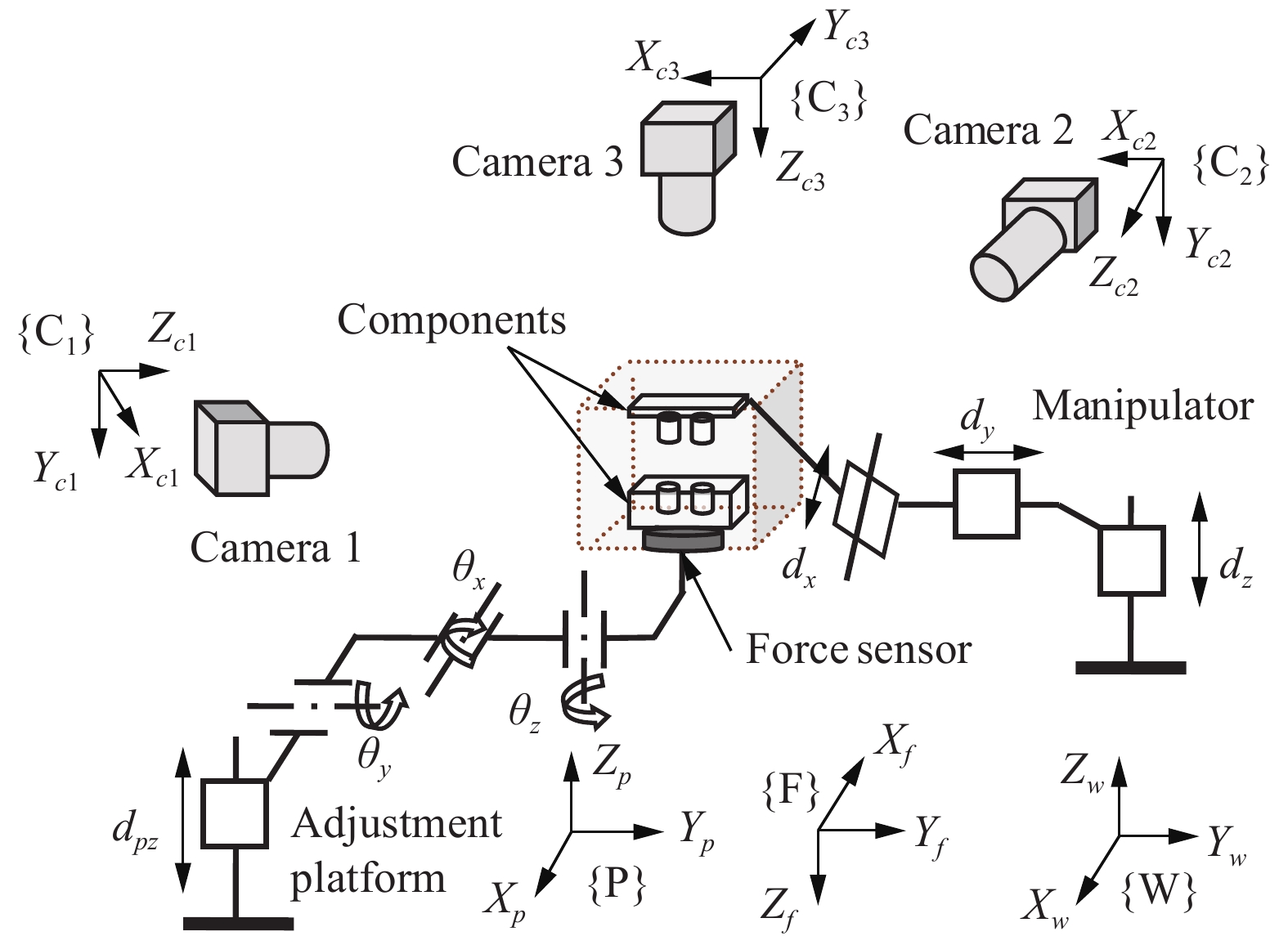
The automated precision assembly system is designed as shown in Fig. 1. It consists of a 4 degree of freedom (DOF) adjustment platform, a 3-DOF manipulator, three microscopic cameras, lighting system and a host computer. The optical axes of three microscopic cameras are approximately orthogonal to each other and the three microscopic cameras can move along their moving platform to adjust the distance between objective lens and objects for capturing clear images. The microscopic camera 1−3 provide mid-view, side-view and up-view of objects.
The world coordinate {W} is established on the base of manipulator. The manipulator can move along Xw, Yw and Zw axes. The platform coordinate {P} is established on the adjustment platform. The 4-DOF adjusting platform consists of three rotation DOFs around Xp, Yp and Zp axes, respectively, and a translation DOF along Zp axis. The camera coordinates {C1}, {C2} and {C3} are established on the three cameras, respectively. The force coordinate {F} is established on the force sensor.
For precision assembly, the goal is to learn the insertion policy through interacting with environment. The insertion process can be modeled as a Markov decision process (MDP). At each time step t, the agent observes a state st
In the insertion task, the state s is defined as
|
st=[fx,fy,fz,pz]T |
(1) |
where fx, fy, and fz are the contact forces along Xf, Yf, and Zf axes, respectively; pz is the insertion depth along Zw axis. The action is defined as
|
at=[dx,dy,dz]T |
(2) |
where dx and dy are the compliant adjustments along Xw and Yw axes, respectively; and dz is the insertion step along Zw axis.
The insertion skill learning framework is based on DDPG, whose framework is shown in Fig. 2. The training process is divided into two stages: expert action learning and self-learning. The final action is composed of two parts: an expert action and a refinement action, which are obtained in the two stages, respectively. In the expert action learning stage, only one expert demonstration is collected and the expert action is learned. In the self-learning stage, the actor and critic networks are further trained with RL through interacting with environment. Besides, efficient exploration strategy is developed to accelerate the training process. After training, the agent obtains the insertion skill and accomplishes the insertion tasks. A skill saving and selection mechanism is designed to improve the adaptability of insertion tasks with different components.
In RL training process, random actions might be harmful to the safety of the robotic system. It is beneficial to learn a stable and safe insertion skill from expert demonstrations. Therefore, a novel framework is proposed to leverage demonstrations and acquire better efficiency.
1) Learning expert action from one-shot demonstration.
A common method to accelerate the RL training process is to pretrain the networks with demonstrations from experts. A large number of demonstrations are usually needed in the pretrain state to obtain adequate performance. However, data collection on real robotic systems is tedious and time-consuming. Therefore, a novel method is proposed to learn a stable and safe expert action from only one demonstration which records the states and the corresponding actions.
In the insertion process, the relationship between contact force and relative translation movements can be modeled with a force Jacobian matrix JF
|
[dxdy]=JF[fxfy]. |
(3) |
JF can be calibrated with the least square method according to the demonstration. The expert action is represented as
|
aet=[dex,dey,dez]T |
(4) |
where dex and dey are the adjustments along Xw and Yw axes, respectively; and dez is the insertion step along Zw axis. dex and dey can be calculated by (5).
|
[dexdey]=−αJF[fxfy] |
(5) |
where α
Then an expert action ate is gotten with only one demonstration. The demonstration data is mainly used to obtain the properties of components by calibrating JF. It is not important whether the demonstration is optimal or not. Therefore, our method is more efficient and convenient than the traditional pretrain-based methods.
2) Neural networks based refinement action
The proposed framework contains two main networks: an actor network and a critic network. The actor network takes a state as input and outputs the refinement action μ(st | θμ) with parameter θμ. There are five fully connected layers in the actor network. The ReLU activation function is used in the first four layers and tanh activation function is used in the last output layer, whose output is the refinement action atr. The final output action at is combined by the expert action ate and refinement action atr,
|
at=ate+atr. |
(6) |
The actions along Xw and Yw axes of final action at are normalized within [−1, 1] and action along Zw axis of at are normalized within [0, 1]. The expert action ate is explainable, safe but not optimal. The refinement action works to improve the insertion efficiency. Then the final action at can meet the requirement of safety and high efficiency.
The critic network takes the state and the refinement action atr as input and outputs the action value Q(st, atr | θQ) with parameter θQ. Two fully connected layers are employed to fuse the state and the action. And two other fully connected layers are used to approximates action value.
A target actor network μ′(st | θμ′) with parameter θμ′ and a target critic network Q′(st, atr | θQ′) with parameter θQ′ are employed to calculate the target values. Their structures are the same as the actor and critic networks, respectively.
3) Preliminaries
During training, the agent samples a minibatch of N state transitions from the replay buffer M to update the parameters of actor and critic networks.
The critic network is trained by minimizing the loss L with parameter θQ:
|
L(θQ)=1NN∑i=1(yi−Q(si,ai|θQ))2 |
(7) |
where yi is computed by
|
yi=RMi+γQ′(si+1,μ′(si+1)|θQ). |
(8) |
RMi is the reward which is detailed in Section 3.2; γ is a discount factor.
The action network is trained by maximizing J(θμ) with parameter θμ:
|
J(θμ)=E[Q(st,μ(st|θμ))]. |
(9) |
The parameters of the actor network are updated by computing the policy gradient with the chain rule:
|
∇θμJ(θμ)=1NN∑i=1[∇aQ(s,a|θQ)|s=si,a=μ(si)×∇θμμ(s|θμ)|s=si]. |
(10) |
The parameters of target networks are updated by slowly tracking the learned networks:
|
{θQ′=τθQ+(1−τ)θQ′θμ′=τθμ+(1−τ)θμ′ |
(11) |
where τ is a factor between 0 and 1.
4) Self-learning stage
During self-learning, the state transitions are collected by interacting with the environment and stored in the memory replay buffer M. The pseudo code of the self-learning stage is given Algorithm 1.
The actor network is trained with
For precision assembly, safety is important and the contact force should be kept within a safe range. Besides, the efficiency is another key factor and it is expected to finish the process with as few insertion steps as possible. Therefore, the designed reward function consists of two parts: the safety reward R1t and the efficiency reward R2t as given in (12).
|
{R1t=1−frtfTR2t=−|dzt−R1(t−1)DT|/DT |
(12) |
where fT is the maximum allowed radial contact force; DT is the maximum allowed insertion depth; frt is the radial contact force after executing the t-th action.
|
frt=√f2xt+f2yt. |
(13) |
Then the reward function RMt is calculated by
|
RMt=R1t+R2t. |
(14) |
The reward R1t means that the agent will receive a small reward if the contact force is large. fr(t-1) can be viewed as the contact force before executing the t-th action. The term R1(t-1)DT provides an expected insertion depth. Larger the current contact force is, smaller the insertion depth should be. And the reward R2t indicates that larger the difference between the real and expected insertion depths is, smaller the reward will be.
Algorithm 1. Self-learning with dynamic exploration
Initialize σa←0.1
Initialize replay buffer M
For episode =1, 2, ···, do:
Reset the initial state s0
For t=1, 2, ···, do:
Compute the expert action ate and refinement action atr
Compute the actions at and atc with (6) and (15)
Execute action atc, observe reward RMt and the next state st+1
If st+1 is a termination state do:
break
End if
Store transition (st, atr, RMt, st+1) in M
Sample a random minibatch of N transitions from M
Calculate gradients and update parameters
Update σa with (17)
st ←st+1
End for
Calculate the cumulative reward and update σa with (16)
End for
When training the RL model, the state space should be explored to improve the performance of the action policy. However, random exploration might be harmful to the safety of the robotic system. For example, the radial contact force may exceed the allowed range. An appropriate exploration strategy can encourage the agent to explore the state space more efficiently. Therefore, we develop an episode-step exploration strategy and the exploration intensity is adjusted online according to the current performance of agent.
Gaussian noise is added to the action for random exploration.
|
act=at+N(0,σaI) |
(15) |
where σa is the standard deviation; atc is the output action with Gaussian noise.
The parameter σa determines the exploration intensity. Generally, the exploration should be increased when the performance of action policy is unsatisfactory. The average episode reward can indicate the performance of action policy. Then a simple but effective episode-based exploration method is given as
|
σa={σt1,if1NsNs∑t=0RMt<0σt2,otherwise |
(16) |
where Ns is the number of steps in the episode; σt1 and σt2 are two thresholds where σt1 > σt2; σa is adjusted after each episode.
The episode-based method is insufficient because σa is only updated after one episode finishes, which is delayed. Then a step-based exploration method is developed which works as a supplement to the episode-based method.
In general, the performance of action atc is expected better than which of the sole expert action ate. Therefore, the expert action ate can be used as an appropriate benchmark to evaluate the performance of the agent after each step. Specifically, if the performance of atc is better than that of ate, the exploration should be decreased for generating stable output. On the contrary, the exploration should be increased for generating a better policy. There is another problem that the real executed action is atc rather than ate, which means the reward Re generated by ate cannot be obtained directly. The reward Re can be estimated with the state before executing action atc. The efficiency part R2t can be calculated by (12). The safety part R1t is calculated with the contact force before rather than after executing atc. Generally, the radial contact force will decrease after executing ate, which means the reward Re calculated by the above method is worse than the real ones. Therefore, the reward Re is competent to work as the benchmark to guide exploration. Then the step exploration method is given as
|
σa←σa−σbtanh(RMt−Re) |
(17) |
where σb is a constant. And σa will be limited within [σmin
In real robotic assembly tasks, the properties of components are different. The model trained with one kind of component might not be suitable for other components. And it is tedious to train a new model for each new component. In order to solve this problem, an insertion skill saving and selection mechanism is developed and the flow chart is given in Fig. 3. Firstly, several typical components are selected and used to train the corresponding models with the proposed methods. Then the trained parameters are saved in a skill pool Sp. The force Jacobian matrix of the i-th model in Sp is denoted as JFi.
Given a new component, one demonstration should be firstly conducted and the force Jacobian matrix JFnew is calibrated. The distance Di between JFnew and JFi is computed by
|
Di=‖JFi−JFnew‖2F. |
(18) |
The model with the minimal distance is chosen as the appropriate model. And the corresponding insertion skill is restored from the skill pool and employed to guide the insertion task with the new component. Therefore, the adaptability for different components is improved.
This section demonstrates the feasibility of the proposed insertion skill learning method in a peg-in-hole assembly simulation environment.
The simulation environment used in this experiment is the same as [21]. The friction coefficient is set to 0.3. The Hookean coefficient is set to 3.3 mN/μm. There are two cylindrical components to be assembled. The heights of the two components are 4 mm. The diameters of the peg and the hole are 4 mm and 4.01 mm respectively.
The training parameters of the proposed insertion skill learning method is given in Table 1. To guarantee the safety of insertion task, the insertion step length dz is limited within [0, 150 μm] and the adjustments dx and dy are limited within [−5 μm, 5 μm]. The maximum allowed radial contact force fT is set to 80 mN. The maximum insertion steps are set to 1000. If radial contact force fr exceeds fT, the insertion task fails. The insertion task succeeds when |fz| > 1000 mN.
| Parameters | Values | Parameters | Values |
| Delayed update rate τ | 0.1 | Discount factor γ | 0.99 |
| Learning rate | 0.001 | Self-learning episodes | 200 |
| Batch size N | 32 | Size of M | 200 |
| Constant α | 0.15 | Thresholds σt1 and σt2 | 0.3, 0.1 |
| Thresholds σmin, σmax | 0.1, 0.5 | Constant σb | 0.3 |
The initial orientation and position errors are set within 0.3 degree and 10 μm, respectively. During self-learning, initial states are sampled randomly within the pose errors range. The test dataset includes 100 initial states with random pose errors. And the trained model is evaluated in the test dataset.
Firstly, one insertion demonstration is conducted. The expert action is learned with the method detailed in Section. 3.1. and evaluated in the test dataset. The success rate is 100%. The mean reward is 0.52. The distribution of radial contact force is shown in Fig. 4. The number of insertion steps is about 54. And the contact force descends below 10 mN after about 10 steps since the beginning of task.
It can be seen the expert action can meet the requirement of safety, but the efficiency is low. Therefore, the performance of the agent should be further improved with the self-learning method introduced in Section. 3.1.
To validate the effectiveness of the proposed dynamic exploration strategy, three different strategies are compared: episode-step exploration, episode exploration and step exploration. The initial insertion depths are set randomly. The self-learning stage terminates after 200 episodes. The training results are shown in Fig. 5. The curve converges after about 25 episodes with the episode-step exploration strategy. In contrast, the curve converges after about 65 and 45 episodes with episode exploration and step exploration, respectively. Compared with episode exploration method, the step exploration method can adjust the exploration intensity in a more timely way. And the convergence speed of step exploration is faster than that of episode exploration. Therefore, the proposed episode-step exploration strategy can improve the training efficiency.
After self-learning, the performance of the agent is evaluated in the test dataset. The mean reward is 0.91 and the success rate is 100%. The number of insertion steps is about 31. The contact force descends below 10 mN after about 3 steps since the beginning of task, which is more efficient than the results of expert action.
The distribution of radial contact force is shown in Fig. 4. The force less than 10 mN occupies over 92% with action at after self-learning. In contrast, it occupies only 55% when using expert action ate. Compared with the expert learning results, the contact force can be kept within a smaller range after self-learning and the performance of the agent has been improved.
The classic DDPG method[11], denoted as comparative method 1, is chosen as a comparative method, and episode exploration strategy is adopted. The structure of the network is the same as which of our method except the expert action part. The robotic assembly method in [21], denoted as comparative method 2, is chosen as another comparative method. In order to compare its performance with our method's, the fuzzy reward system is replaced with our reward function. And the other parts are the same as which of the original method in [21].
The training process finishes after 200 episodes. The training result is shown in Fig. 6. The convergence speed of comparative method 2 is much faster than which of comparative method 1. But the curve of method 2 is always below which of our method. Then the trained models are evaluated in the test dataset. The final performance of comparative methods 1 and 2 are similar. The success rates are both 100%. The mean rewards are 0.89 and 0.86, respectively. The mean reward of our method is 0.91, given in Section 4.3, which is better than the two comparative methods′. Some comparative results are given in Table 2. The average radial contact force (ACF) is computed in each insertion task. And the mean and standard deviation (STD) of ACFs are computed. The mean and STD of steps are also computed. The four values of our method are smaller than the two comparative methods.
| Methods | Mean of ACF (mN) | STD of ACF(mN) | Mean of Steps | STD of Steps |
| Our method | 5.53 | 1.26 | 30.21 | 0.43 |
| Comparative method 1 | 6.77 | 1.34 | 32.58 | 0.59 |
| Comparative method 2 | 10.13 | 1.66 | 34.32 | 0.65 |
Our method outperforms the two comparative methods and the reasons are given as follows. As for the comparative method 1, the exploration strategy is worse than ours. Besides, our framework contains an expert action and a refinement action, which can accelerate the training process. As for the comparative method 2, the acquisition of expert action is improper. It views the contact force as decoupled, which is not always the truth. And the variance of action space noise decreases all the time. On the contrary, our method can adjust the exploration intensity more flexibly. Furthermore, the two comparative methods should retrain the models when meeting new components. However, in our method, a skill pool is established with the force Jacobian matrix, and the most appropriate model will be selected from the skill pool to directly accomplish the new insertion tasks. And the gap between simulation and real robotic system can be bridged with the method detailed in Section 5.2, which is based on the force Jacobian matrix. But the two comparative methods cannot do that. Therefore, the adaptability of our method is much better.
In real robotic applications, the properties of components may be different and it is time-consuming to train a new model for each new component. The method, detailed in Section. 3.4, can solve this problem. In order to validate the performance of the method, a set of experiments are conducted. Three typical components are chosen and the Hookean coefficient are 0.5k0, k0 and 2k0, respectively. k0 is the Hookean coefficient used in the aforementioned experiments. These models are trained with the method introduced in Section 3 and are saved to the skill pool Sp.
A new component is chosen as a test component and the Hookean coefficient is 2.2k0. The distance Di, i=1, 2, 3 is computed with (18). And D3 is the smallest distance and the third model is chosen as the most appropriate model. Then the model is evaluated in the test dataset. The mean reward is 0.924 and the success rate is 100%. The results are given in Table 3. The models 1−3 are the three models in the skill pool. We test the two other models with the new component and the mean rewards decrease obviously. It validates the correctness of choosing the third model for insertion tasks with the new component. Therefore, it is important to choose an appropriate model to obtain better performance. And the proposed method provides a convenient and efficient approach for insertion tasks with a new component.
| Models | Success rate | Mean reward |
| Model 1 | 0.98 | 0.75 |
| Model 2 | 1.0 | 0.84 |
| Model 3 | 1.0 | 0.92 |
An experiment system is established according to the scheme given in Section 2.1, as shown in Fig. 7. In this experiment system, camera 1 and camera 2 are GC2450 cameras and camera 3 is a PointGrey camera. All the three cameras are equipped with Navitar zoom lens with magnification 0.47~4.5×, which capture images 15 frames per second with image size of 2448×2050 in pixel. The adjustment platform is composed of a Micos WT-100 for rotation around Xp and Yp axes, Sigma SGSP-40YAW for around Zp axis Micos ES-100 for translation along Zp axis. The rotation and translation resolutions of adjustment platform are 0.001 degree, 0.02 degree, 0.02 degree. and 1 μm, respectively. The manipulator is composed of a Sugura KWG06030G for translation along Xw, Yw and Zw axes with resolution 1 μm.
Three kinds of components are employed to verify the effectiveness of the proposed insertion skill learning method. The insertion tasks are to insert the components A, B and C into the component D. The components A, B and C are electronic components. The component D is a bread board and there are many holes on it. The components A, B, and C are separately mounted on the manipulator in sequence, and component D is mounted on the adjustment platform. The diameters of the pegs are 1 mm. The height of the components A, B, and C are 5 mm, 8 mm and 5 mm, respectively. The vision-based pose alignment is conducted before the insertion process[1]. The force sensor provides contact force during insertion tasks.
Usually, it takes many hours to train the RL model to obtain insertion skills on real robotic systems. It is very time-consuming and the safety cannot be guaranteed. In order to solve this problem, we proposed a method to bridge the gap between simulation and the real robotic system. And the insertion skills obtained in the simulation environment can be directly used on real robotic systems by using our method.
In real robotic systems, the coordinates of force sensor and manipulator may not be identical. JX is the inverse of JF. and can indicate the relationship between relative movements and contact force. Then a new simulation environment can be established, which is similar to the real robotic environment.
The components A and B are separately mounted on the manipulator in sequence and the relative movements of the manipulator will cause deformation offset of the components. The corresponding force Jacobian matrices of components A and B are given in (19) and (20).
|
JFA=[−0.1330−0.0101−0.00410.0631]μm/mN |
(19) |
|
JFB=[−0.2328−0.0321−0.03650.5251]μm/mN |
(20) |
where JFA and JFB are the force Jacobian matrices of components A and B, respectively.
The components A and B are trained in the corresponding simulation environments and the corresponding model A and model B are saved in the skill pool. Four experiments are conducted for each component with the learned insertion policy. And all of the eight experiments finished successfully. The distributions of the contact force are given in Fig. 8. In the insertion tasks with component A, the contact force less than 50 mN occupies over 90%. As for component B, the contact force less than 30 mN occupies over 95%. The success of the experiments validates the effectiveness of our method. It can save a lot of time and provide a much more convenient way to train RL model for assembly tasks on real robotic system.
In order to further validate the feasibility of the skill saving and selection mechanism, the component C is viewed as a new component used in the insertion tasks. The component C is mounted on manipulator and the relative movements of manipulator will cause deformation offset of the component. The corresponding force Jacobian matrix JFC is firstly obtained and given in (21).
|
JFC=[−0.23040.0237−0.00010.2584]μm/mN. |
(21) |
There are two trained models, model A and model B, in the skill pool. The distance, {Di| i=1, 2}, between JFC and the force Jacobian matrices of two models are computed with (18). The materials of components A and C are similar, and as expected, D1 is smaller than D2. Then the model A is selected to complete the insertion tasks with component C. The maximum insertion step is set as 50 μm. Four experiments are conducted with different initial states. Some details of one insertion task are shown in Fig. 9. The contact force fx and fy are kept within a safe range during the insertion process. Adjustments dx and dy are employed to reduce the contact force. The insertion step dz decreases as the contact force increases. The distribution of the radial contact force is shown in Fig. 8. The contact force less than 30 mN occupies over 96%. The above results verify the feasibility of the skill saving and selection mechanism which promotes the adaptability to new components.
A DDPG-based skill learning framework is proposed for robotic insertion. Considering both the safety and efficiency, the action to be executed is composed of two parts: an expert action and a refinement action, which are learned from one demonstration and RL, respectively. The episode-step exploration strategy is designed to improve training efficiency of RL. In order to improve the adaptability of the insertion skill learning method, a skill saving and selection mechanism is designed. It is convenient to select an appropriate model from the skill pool to execute insertion tasks when meeting new components. To bridge the gap between simulation and real robotic systems, a simulation environment is established under the guidance of force Jacobian matrix. Then the models can be trained in the simulation environment and be used directly in the real insertion tasks. The results of simulations and experiments show the effectiveness of the proposed insertion skill learning framework.
This work was supported by National Key Research and Development Program of China (No.2018AAA0103005) and National Natural Science Foundation of China (No. 61873266).
|
S. Liu, D. Xu, D. P. Zhang, Z. T. Zhang. High precision automatic assembly based on microscopic vision and force information. IEEE Transactions on Automation Science and Engineering, vol. 13, no. 1, pp. 382–393, 2016. DOI: 10.1109/TASE.2014.2332543.
|
|
J. Zhang, D. Xu, Z. T. Zhang, W. S. Zhang. Position/force hybrid control system for high precision aligning of small gripper to ring object. International Journal of Automation and Computing, vol. 10, no. 4, pp. 360–367, 2013. DOI: 10.1007/s11633-013-0732-y.
|
|
F. B. Qin, D. Xu, D. P. Zhang, Y. Li. Robotic skill learning for precision assembly with microscopic vision and force feedback. IEEE/ASME Transactions on Mechatronics, vol. 24, no. 3, pp. 1117–1128, 2019. DOI: 10.1109/TMECH.2019.2909081.
|
|
M. Armin, P. N. Roy, S. K. Das. A survey on modelling and compensation for hysteresis in high speed nanopositioning of AFMs: Observation and future recommendation. International Journal of Automation and Computing, vol. 17, no. 4, pp. 479–501, 2020. DOI: 10.1007/s11633-020-1225-4.
|
|
K. G. Zhang, J. Xu, H. P. Chen, J. G. Zhao, K. Chen. Jamming analysis and force control for flexible dual peg-in-hole assembly. IEEE Transactions on Industrial Electronics, vol. 66, no. 3, pp. 1930–1939, 2019. DOI: 10.1109/TIE.2018.2838069.
|
|
S. Liu, Y. F. Li, D. P. Xing. Sensing and control for simultaneous precision peg-in-hole assembly of multiple objects. IEEE Transactions on Automation Science and Engineering, vol. 17, no. 1, pp. 310–324, 2020. DOI: 10.1109/TASE.2019.2921224.
|
|
F. Chen, F. Cannella, J. Huang, H. Sasaki, T. Fukuda. A study on error recovery search strategies of electronic connector mating for robotic fault-tolerant assembly. Journal of Intelligent &Robotic Systems, vol. 81, no. 2, pp. 257–271, 2016. DOI: 10.1007/s10846-015-0248-5.
|
|
D. P. Xing, Y. Lv, S. Liu, D. Xu, F. F. Liu. Efficient insertion of multiple objects parallel connected by passive compliant mechanisms in precision assembly. IEEE Transactions on Industrial Informatics, vol. 15, no. 9, pp. 4878–4887, 2019. DOI: 10.1109/TII.2019.2897731.
|
|
J. Takahashi, T. Fukukawa, T. Fukuda. Passive alignment principle for robotic assembly between a ring and a shaft with extremely narrow clearance. IEEE/ASME Transactions on Mechatronics, vol. 21, no. 1, pp. 196–204, 2016. DOI: 10.1109/TMECH.2015.2448639.
|
|
V. Mnih, K. Kavukcuoglu, D. Silver, A. A. Rusu, J. Veness, M. G. Bellemare, A. Graves, M. Riedmiller, A. K. Fidjeland, G. Ostrovski, S. Petersen, C. Beattie, A. Sadik, I. Antonoglou, H. King, D. Kumaran, D. Wierstra, S. Legg, D. Hassabis. Human-level control through deep reinforcement learning. Nature, vol. 518, no. 7540, pp. 529–533, 2015. DOI: 10.1038/nature14236.
|
|
T. P. Lillicrap, J. J. Hunt, A. Pritzel, N. Heess, T. Erez, Y. Tassa, D. Silver, D. Wierstra. Continuous control with deep reinforcement learning. In Proceedings of the 4th International Conference on Learning Representations, San Juan, Puerto Rico, 2016.
|
|
J. L. Luo, E. Solowjow, C. T. Wen, J. A. Ojea, A. M. Agogino, A. Tamar, P. Abbeel. Reinforcement learning on variable impedance controller for high-precision robotic assembly. In Proceedings of the International Conference on Robotics and Automation, IEEE, Montreal, Canada, pp. 3080−3087, 2019. DOI: 10.1109/ICRA.2019.8793506.
|
|
T. Johannink, S. Bahl, A. Nair, J. L. Luo, A. Kumar, M. Loskyll, J. A. Ojea, E. Solowjow, S. Levine. Residual reinforcement learning for robot control. In Proceedings of International Conference on Robotics and Automation, IEEE, Montreal, Canada, pp. 6023−6029, 2019. DOI: 10.1109/ICRA.2019.8794127.
|
|
T. Inoue, G. De Magistris, A. Munawar, T. Yokoya, R. Tachibana. Deep reinforcement learning for high precision assembly tasks. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, Vancouver, Canada, pp. 819−825, 2017. DOI: 10.1109/IROS.2017.8202244.
|
|
F. M. Li, Q. Jiang, S. S. Zhang, M. Wei, R. Song. Robot skill acquisition in assembly process using deep reinforcement learning. Neurocomputing, vol. 345, pp. 92–102, 2019. DOI: 10.1016/j.neucom.2019.01.087.
|
|
Y. X. Fan, J. L. Luo, M. Tomizuka. A learning framework for high precision industrial assembly. In Proceedings of International Conference on Robotics and Automation, IEEE, Montreal, Canada, pp. 811−817, 2019. DOI: 10.1109/ICRA.2019.8793659.
|
|
M. Vecerik, O. Sushkov, D. Barker, T. Rothörl, T. Hester, J. Scholz. A practical approach to insertion with variable socket position using deep reinforcement learning. In Proceedings of International Conference on Robotics and Automation, IEEE, Montreal, Canada, pp. 754−760, 2019. DOI: 10.1109/ICRA.2019.8794074.
|
|
J. L. Luo, E. Solowjow, C. G. Wen, J. A. Ojea, A. M. Agogino. Deep reinforcement learning for robotic assembly of mixed deformable and rigid objects. In Proceedings of IEEE/RSJ International Conference on Intelligent Robots and Systems, IEEE, Madrid, Spain, pp. 2062−2069, 2018. DOI: 10.1109/IROS.2018.8594353.
|
|
G. Thomas, M. Chien, A. Tamar, J. A. Ojea, P. Abbeel. Learning robotic assembly from CAD. In Proceedings of IEEE International Conference on Robotics and Automation, IEEE, Brisbane, Australia, pp. 3524−3531, 2018. DOI: 10.1109/ICRA.2018.8460696.
|
|
Z. M. Hou, H. M. Dong, K. G. Zhang, Q. Gao, K. Chen, J. Xu. Knowledge-driven deep deterministic policy gradient for robotic multiple peg-in-hole assembly tasks. In Proceedings of IEEE International Conference on Robotics and Biomimetics, IEEE, Kuala Lumpur, Malaysia, pp. 256−261, 2018. DOI: 10.1109/ROBIO.2018.8665255.
|
|
J. Xu, Z. M. Hou, W. Wang, B. H. Xu, K. G. Zhang, K. Chen. Feedback deep deterministic policy gradient with fuzzy reward for robotic multiple peg-in-hole assembly tasks. IEEE Transactions on Industrial Informatics, vol. 15, no. 3, pp. 1658–1667, 2019. DOI: 10.1109/TII.2018.2868859.
|
| 1. | Chi Zhang, Wei Zou, Ningbo Cheng, et al. Towards Jumping Skill Learning by Target-guided Policy Optimization for Quadruped Robots. Machine Intelligence Research, 2024. DOI:10.1007/s11633-023-1429-5 |
| 2. | Jingqing Ruan, Kaishen Wang, Qingyang Zhang, et al. Learning Top-K Subtask Planning Tree Based on Discriminative Representation Pretraining for Decision-making. Machine Intelligence Research, 2024, 21(4): 782. DOI:10.1007/s11633-023-1483-z |
| 3. | Qi-Yue Yin, Jun Yang, Kai-Qi Huang, et al. AI in Human-computer Gaming: Techniques, Challenges and Opportunities. Machine Intelligence Research, 2023, 20(3): 299. DOI:10.1007/s11633-022-1384-6 |
| 4. | Linghui Meng, Muning Wen, Chenyang Le, et al. Offline Pre-trained Multi-agent Decision Transformer. Machine Intelligence Research, 2023, 20(2): 233. DOI:10.1007/s11633-022-1383-7 |
| 5. | Íñigo Elguea-Aguinaco, Antonio Serrano-Muñoz, Dimitrios Chrysostomou, et al. A review on reinforcement learning for contact-rich robotic manipulation tasks. Robotics and Computer-Integrated Manufacturing, 2023, 81: 102517. DOI:10.1016/j.rcim.2022.102517 |
| 6. | Chun Yang, Chang Liu, Xu-Cheng Yin. Weakly Correlated Knowledge Integration for Few-shot Image Classification. Machine Intelligence Research, 2022, 19(1): 24. DOI:10.1007/s11633-022-1320-9 |
| 7. | Yuze Jiang, Zhouzhou Huang, Bin Yang, et al. A review of robotic assembly strategies for the full operation procedure: planning, execution and evaluation. Robotics and Computer-Integrated Manufacturing, 2022, 78: 102366. DOI:10.1016/j.rcim.2022.102366 |
| 8. | Yansong Wu, Fan Wu, Lingyun Chen, et al. 1 kHz Behavior Tree for Self-adaptable Tactile Insertion. 2024 IEEE International Conference on Robotics and Automation (ICRA), DOI:10.1109/ICRA57147.2024.10610835 |
| Parameters | Values | Parameters | Values |
| Delayed update rate τ | 0.1 | Discount factor γ | 0.99 |
| Learning rate | 0.001 | Self-learning episodes | 200 |
| Batch size N | 32 | Size of M | 200 |
| Constant α | 0.15 | Thresholds σt1 and σt2 | 0.3, 0.1 |
| Thresholds σmin, σmax | 0.1, 0.5 | Constant σb | 0.3 |
| Methods | Mean of ACF (mN) | STD of ACF(mN) | Mean of Steps | STD of Steps |
| Our method | 5.53 | 1.26 | 30.21 | 0.43 |
| Comparative method 1 | 6.77 | 1.34 | 32.58 | 0.59 |
| Comparative method 2 | 10.13 | 1.66 | 34.32 | 0.65 |
| Models | Success rate | Mean reward |
| Model 1 | 0.98 | 0.75 |
| Model 2 | 1.0 | 0.84 |
| Model 3 | 1.0 | 0.92 |